|
FRONTESPIZIO - Primo folio (non numerato), recto |
FRONTISPIECE - First folio (unnumbered), recto |
|
|
Frontispiece  Diſciplinæ Mathematicæ loquuntur[.] Qui cupitis Rerum varias cognoſcere cauſaſ[.] Diſcite noſ, cunctiſ hac patet una uia. |
 The Mathematical Disciplines say, whoever strives to investigate the reasons to think, study us, this way is open to everyone. |
|
INCIPIT - Primo folio (non numerato), verso |
INCIPIT - First folio (unnumbered), verso |
|
|
Incipit INVENTIONE DE NICOLO TARTAGLIA Briſciano Intitolata Scientia Noua diuiſa in V libri, nel Primo di quali ſe dimoſtra theoricamente, la natura, & effetti de corpi egualmente graui, in li dui contrarii moti che in eſſi puon accadere, & de lor contrarii effetti. In lo ſecondo (geometricamente) ſe approua, e dimoſtra la qualita ſimilitudine, et proportionalita di tranſiti loro ſecondo li uarij modi, che puono eſſer eietti, ouer tirati uiolentemente per aere, et ſimilmente delle lor diſtantie. In lo terzo ſe inſegna una noua pratica de miſurare con l’aſpetto, le altezze diſtantie ypothumiſſale, et orizontale delle coſe apparente, giontoui anchora la theorica, cioe la ragione et cauſa di tal operare. In lo quarto ſe dara la proportione de l’ordine dil creſcere callar che in ogni pezzo di artegliaria nelli ſuoi tiri, alzandolo ouer arbaſſandolo, ſopra il pian de l’orizonte, et ſimilmente ogni mortaro, anchora ſe inſegnara il modo di trouar tutte le dette uarieta, ouer quantita de tiri in ogni pezzo de artegliaria, ouer mortaro mediante la notitia dun tiro ſolo. Anchora ſi mostrara il modo come ſi debbia gouernar un bombardiero quando deſidera, di battere ouer di percottere in qual che luoco apparente. Oltra di queſto ſe inſegnara anchora il modo come ſi debbia gouernar il detto bombardiero quando gli fuſſe fatto un riparo dauanti al luoco doue percote uolendo pur percottere nel medemo luoco per altra uia, ouer elleuatione quantunque piu non ueda quel tal luoco. Anchora ſe dara il modo di ſapere percottere continuamente la oſcura notte in un luoco appoſtato il giorno auanti. |
INVENTION OF NICOLO TARTAGLIA from Brescia entitled Nova scientia, divided into five books.1 In the first book, the nature and effects of equally heavy bodies are theoretically demonstrated as well as the two contrary motions that can affect such bodies and the contrary effects of such motions. In the second [book], the qualities, similarities and proportions of the transits, and therefore of the distances, of such bodies are shown and demonstrated (geometrically) according to the various ways in which the bodies can be ejected, that is, thrown violently through the air. In the third [book], a new practice to measure by sight the height and the diametral and horizontal distances of the perceptible objects is taught. The theory, that is, the reason and the cause of such operations, is also added. In the fourth [book], the ratio is described between the increase [and] decrease of the shots of each piece of artillery and the elevating or lowering of the piece above the plane of the horizon. Similarly [the same will be shown] for each [type of] mortar. Moreover, the method of how to find all the mentioned varieties is taught, that is, the quantitative information concerning the shots of each piece of artillery and mortar on the basis of information concerning one single shot. In addition, the method is given of how a bombardier must proceed when he intends to hit or strike a certain perceptible place. In addition, the method is also taught of how the mentioned bombardier should proceed when the place he intends to strike has been covered with a protective shield [so that he can] strike it using another path, that is, using another elevation, even though he is no longer able to see that place. Again, the method is shown of how to continuously strike during the night a place that has been targeted earlier in the day. |
|
INCIPIT - Primo folio (non numerato), verso - cont. |
INCIPIT - First folio (unnumbered), verso - cont. |
|
|
In lo quinto libro ſe dechiarira (ſecondo l’autorita de molti Eccellentiſſimi Naturali) la natura, et origine de diuerſe ſpecie di gome, olei, acque ſtillate, anchora de diuerſi ſimplici minerali et non minerali dalla natura prodotti, et da l’arte fabricati, anchora ſe manifeſtara alcune ſue particolare proprieta circa a larte de fuochi. Et ſimilmente ſe delucidara quale ſono quelle materie chi ſe conuiengono et che ſe accordano et quale ſono quelle che non ſi conuiengono ne ſe accordano, a ardere inſieme, et conſequentemente ſe dara il modo di componere, uarie et diuerſe ſpecie de fuochi, non ſolamente alla defenſione de ogni murata terra utiliſſimi, ma anchora in molte altre occorentie molto a propoſito. |
The fifth book discloses (according to the authority of many very Excellent Naturals2) the nature and the origin of several kinds of gum, oil, distilled water, and also several simple and not simple minerals produced by nature and manufactured by art. Then, some particular characteristics of the art of the fires3 are clarified. Similarly, it is then explained which materials burn well together and which materials are not appropriate for this purpose. Consequently, the method is described of how to compound various and different kinds of fires, which are not only very useful for defending fortified land, but also very appropriate for many other occasions. |
|
EPISTOLA - Secondo folio (non numerato), recto |
EPISTLE - Second folio (unnumbered), recto |
|
|
ALLO ILLVSTRISSIMO ET INVICTISSIMO SIgnor Franceſcomaria Feltrenſe dalla Rouere Duca Eccellentiſſimo di Vrbino et di Sora, Conte di Montefeltro, et di Durante. Signor di Senegaglia, et di Peſaro. Prefetto di Roma, et dello Inclito Senato Venetiano Digniſſimo General Capitano. Epistle HABITANDO in Verona l’Anno MDXXXI Illuſtriſſimo. S. Duca mi fu adimandato da uno mio intimo et cordial amico Peritisſimo bombardiero in castel uecchio (huomo atempato et copioſo di molte uirtu) dil modo di mettere a ſegno un pezzo de artegliaria al piu che puo tirare. E a ben che in tal arte io non haueſſe pratica alcuna (perche in uero Eccellente Duca) giamai diſgargeti artegliaria, archibuſo, bombarda, ne ſchioppo niente dimeno (deſideroſo di ſeruir l’amico) gli promisſi di darli in breue riſſoluta riſposta. Et dipoi che hebbi ben masticata et ruminata tal materia, gli concluſi, et dimoſtrai con ragioni naturale, et geometrice, qualmente biſognaua che la bocca del pezzo steſſe elleuata talmente che guardaſſe rettamente a 45 gradi ſopra a l’orizonte, et che per far tal coſa iſpedientemente biſogna hauere una ſquara de alcun metallo ouer legno ſodo che habbia interchiuſo un quadrante con lo ſuo perpendicolo come di ſotto appar in diſegno, et ponendo poi una parte della gamba maggiore di quella (cioe la parte BE) ne l’anima ouer bocca dil pezzo disteſa rettamente per il fondo dil uacuo della canna, alzando poi tanto denanti il detto pezzo che il perpendicolo HD ſeghi lo lato curuo EGF (dil quadrante) in due parti eguali (cioe in ponto G) All’hora ſe dira che il detto pezzo guardara rettamente a 45 gradi ſopra a l’orizonte. Perche (Signor clarisſimo) il lato curuo EGF del quadrante (ſecondo li aſtronomi) 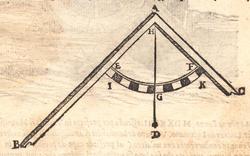
|
TO THE MOST ILLUSTRIOUS AND HIGHLY RESPECTED Lord Francescomaria Feltrense Della Rovere, Very Excellent Duke of Urbino and of Sora, Count of Montefeltro and of Durante, Lord of Senigallia and of Pesaro, Prefect of Rome and Very Worthy General Captain of the Illustrious Senate of Venice. During the year 1531, when the Most Illustrious Lord Duke was living in Verona, I was asked by a close and kind friend of mine, a very skilled bombardier at the Castel Vecchio4 (an aged man with many virtues), about the method to set up a piece of artillery in such a way that it shoots the farthest. Although I did not have any experience in such an art (because the truth is, Very Excellent Duke, I have never discharged any artillery, or harquebus, or bombard or rifle5), I nevertheless (as I wished to serve a friend) promised to quickly provide him with a resolute answer. After I had carefully contemplated and ruminated this subject, I concluded and demonstrated to him by means of natural and geometrical arguments that the mouth of the piece had to be elevated so that it addresses straightly [the inclination of] 45 degrees above the horizon. Moreover, [I told him] that to accomplish this quickly, a square of whichever metal or hardwood is needed. The square must contain a quadrant with its plumb line [positioned] as it appears below in the drawing. Then, one inserts part of the longer side of the square (that is the part BE) into the bore or mouth of the piece, laying it flat along the bottom of the empty barrel, and one lifts up the front of the mentioned piece until the plumb line HD divides the curved side EGF (of the quadrant) into two equal parts (that is at the point G). At this point, one can say that the mentioned piece is straightly elevated at 45 degrees above the horizon. Since (Very Illustrious) the curved side EGF of the quadrant is (according to the astronomers) 
|
|
EPISTOLA - Secondo folio (non numerato), verso |
EPISTLE - Second folio (unnumbered), verso |
|
|
ſe diuide in 90 parti eguale, et cadauna di quelle chiamano grado. Pero la mita di quello (cioe GF) uerria a eſſer gradi 45. Ma per acordarſe con quello che ſe ha da dire lo hauemo diuiſo in 12 parti eguali, et accioche uoſtra Illuſtriſsima D. S. ueda in figura quello che diſopra hauemo con parole depinto hauemo qua diſotto deſignato il pezzo con la ſquara in bocca aſſettato ſecondo il propoſito da noi conchiuſo al detto noſtro amico. La qual concluſion a eſſo parſe hauer qualche conſonantia pur circa cio dubitaua alquanto parendo a lui che tal pezzo guardaſſe troppo alto. Il che procedeua per non eſſer capace delle nostre ragioni, ne in le Mathematice ben corroborrato, niente di meno con alcuni iſperimenti particolari in fine ſe uerifico totalmente coſi eſſere. Pezzo elleuato alli 45 gradi ſopra a l’orizonte. 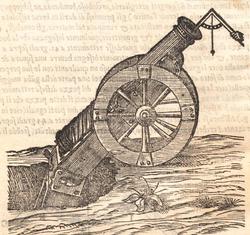 Ma piu ne l’anno MDXXXII eſſendo per prefetto in Verona il Magnifico miſſer Leonardo Iuſtiniano. Vn capo de bombardieri amiciſſimo di quel nostro amico. Venne in concorrentia con un’altro (al preſente capo de bombardieri in Padoa) et un giorno accadete che fra loro fu proposto il medemo che a noi propoſſe quel noſtro amico, cioe a che ſegno ſi doueſſe aſſetare un pezzo de artegliaria che faceſſe |
divided into ninty equal parts and each of these is called a degree, then its half (that is GF) is 45 degrees. Appropriately to what we have to say,6 we [however] divide it [the quadrant] into twelve equal parts. To let Your Most Illustrious Ducal Lordship see in a figure what we have described above in words, we have drawn the piece [of artillery] with the square placed in the mouth of the piece in a figure below, positioned according to the argument concluded for our mentioned friend. Although it seemed to him that this conclusion contains some truth, he nevertheless suspected that the piece was elevated too much. This occurred because he was unable to understand our arguments and because he was not practiced in mathematics. In the end, however, the truth of the argument was verified by means of certain specific experiments. A piece elevated at 45 degrees above the horizon.  During the year 1532, moreover, the Prefect of Verona was the Magnificent Sir Leonardo Iustiniano, chief bombardier and very close friend of our friend. He and another (now chief bombardier in Padoa) challenged each other and one day happened to argue about the same question suggested to us by our friend, that is, the elevation at which a piece of artillery has to be set in order to accomplish |
|
EPISTOLA - Terzo folio (non numerato), recto |
EPISTLE - Third folio (unnumbered), recto |
|
|
il maggior tiro che far poſſa ſopra un piano. Quel amico di quel nostro amico gli concluſe con una ſquara in mani il medemo che da noi fu terminato cioe come di ſopra hauemo detto et deſignato in figura. L’altro diſſe che molto piu tiraria a dui ponti piu baſſo di tal ſquara (la quale era diuiſa in 12 parti) come diſotto appare in diſegno.  Et ſopra di questo fu depoſta una certa quantita de danari, et finalmente ueneno alla ſperientia, et fu condotta una colobrina da 20 a Santa Lucia in campagna, et cadauno di loro tiro ſecondo la propoſta ſenza alcun auantaggio di poluere ne di balla, onde Quello che tiro ſecondo la nostra determinatione, tirò di lontano (ſecondo che ne fu referto) pertiche 1972 da piedi 6 per pertica, alla ueroneſa, l’altro che tirò li dui ponti piu baſſo, tirò di lontano ſolamente pertiche 1872 per la qual coſa tutti li bombardieri, et altri ſe uerificorno della noſtra determinatione, che auanti di queſta iſperientia ſtaſeuano ambigui imo la maggior parte haueuano contraria opinione parendoli che tal pezzo guardaſſe tropo alto. Ma piu forte uoglio che uostra preclariſsima Signoria ſappia che di tre coſe è forza che ne ſia una, ouer che li miſuranti ferno errore nel miſurare, ouer che a me non fu refferto il uero, ouer che il ſecondo cargo piu diligentemente dil primo. Perche la ragione ne demostra |
the longest possible shot over a plane. That friend of our friend with a square in his hands came to the same conclusion we did, that is, as we said above and drew in the figure. The other [bombardier] said that it would project much further were it set two points lower within that square (which was divided into twelve parts) as it appears in the drawing below.  A certain quantity of money was bet on this [question] and they finally arrived at the experiment. A culverin of twenty [libra] was brought to the countryside around Santa Lucia.7 Each of them shot according to what they suggested and without any difference in reference to the ball and to the charge. The one who shot according to our conclusion reached (according to what was referred) 1972 perches, [where] each perch is [constituted] of six feet of [the measurement system of] Verona. The other, who shot two points lower, reached only 1872 perches. For this reason, all the bombardiers and the other persons recognized the truth of our conclusion, although before the experiment they had doubted it and most of them had been of the contrary opinion as it seemed to them that the piece was elevated too much. But I want Your Most Illustrious Lordship to understand the subject better and of the three [following] statements it is necessary that only one is true: either the measurers made a mistake while measuring, or I was not told the truth, or the second charge was more diligently prepared than the first. Because8 according to the argument it is demonstrated |
|
EPISTOLA - Terzo folio (non numerato), verso |
EPISTLE - Third folio (unnumbered), verso |
|
|
che il ſecondo (cioe quello che tiró li dui ponti piu baſſo[)] [tirò] alquanto piu dil dovere alla proportione del primo, ouer che il primo tirò alquanto manco di quello che doueua tirare alla proportione del ſecondo, come nel quarto libro (doue trattaremo de la proportion di tiri) in breue quella potra conoſcere e uedere. Et ſappia uostra Magnanimita che per eſſer stato all’hora in tal materia desto deliberai di uoler piu oltra tentare. Et cominciai (et non ſenza ragione) a inuiſtigare le ſpecie di moti che in un corpo graue poteſſe accadere, onde trouai quelle eſſere due cioe naturale, et uiolente, et quegli trouai eſſer totalmente in accidenti contrarij mediante li lor contrarij effetti, ſimilmente trouai con ragione a l’intelletto euidente eſſer impoſſibile mouerſi un corpo graue di moto naturale et violente inſieme miſto Dapoi inueſtigai con ragione geometrice demoſtratiue la qualita di tranſiti, ouer moti uiolenti de detti corpi graui, ſecondo li uarij modi che pono eſſer eietti, ouer tirati uiolentemente per aere. Oltra di queſto me certificai con ragioni geometrice demoſtratiue. Qualmente tutti li tiri de ogni ſorte artegliarie, ſi grande come piccole egualmente elleuate ſopra il pian de l’orizonte, ouer egualmente oblique, ouer per il pian de l’orizonte, eſſer fra loro ſimili et conſequentemente proportionali, et ſimilmente le distantie loro. Dapoi conobbi con ragion naturale qualmente la diſtantia del ſopra detto tiro elleuato alli 45 gradi ſopra a l’orizonte, era circa decupla al tramito retto dun tiro fatto per il piano de l’orizonte, che da bombardieri è detto tirar de ponto in bianco, con la qual euidentia Magnanimo Duca trouai con ragioni geometrice et algebratice qualmente una balla tirata uerſo li detti 45 gradi ſopra a l’orizonte ua circa a quattro uolte tanto per linea retta di quello che ua eſſendo tirata per il pian de l’orizonte che da bombardieri è chiamato (come ho detto) tirar de ponto in bianco. Per il che ſi manifeſta qualmente una balla tirata da una medema artegliaria ua piu per linea retta per un uerſo che per un’altro, et conſequentemente fa maggior effetto. |
that according to the ratio of the first [shot], the second [shot] (that is, the one that was shot two points lower[)] was shot farther or that according to the ratio of the second [shot] the first one was shot less far, as you will soon know and see in the fourth book (where we will speak about the ratios among the shots). Your Magnanimity should also know that, as I had entered [the investigation of] this matter by that time, I decided to investigate9 further. I started (not without reason) to investigate the kinds of motions that take place when a heavy body is involved. I found that there are two kinds [of motion]:10 the natural and the violent. I also found that, in reference to their accidents,11 they are completely contrary to each other because of their contrary effects. Similarly, with an argument evident to the intellect, I found it is impossible for a heavy body to move according to natural and violent motion mixed together. Then12 by means of geometrical and demonstrative arguments, I investigated the qualities of the transits, that is, of the violent movements of the mentioned heavy bodies in reference to the different ways in which they can be projected or violently thrown through the air. Besides this, using geometric and demonstrative arguments, I certified that all the shots of all kinds of artillery, large as well as small and equally elevated above the horizon or equally oblique13 or parallel to the plane of the horizon, are similar to each other and consequently also proportional to each other. Similarly, [the same is true] for their ranges. Then,14 using natural arguments,15 I found that the range of the above-mentioned shot elevated at 45 degrees above the horizon was ten times the straight transit of a shot made parallel to the plane of the horizon, which is said by the bombardiers shooting at the blank point. On the basis of this evidence, Magnanimous Duke, using means of geometric and algebraic arguments, I found that a ball thrown along the mentioned 45 degrees above the horizon moves along a straight line which is about four times the straight line along which a ball moves when thrown parallel to the plane of the horizon, called by the bombardiers (as I said) shooting at the blank point. From this, it also becomes clear16 that a ball thrown by the same artillery follows a longer straight line in a certain way than in others and, consequently, produce more [destructive] effect. |
|
EPISTOLA - Terzo folio (non numerato), verso - cont. |
EPISTLE - Third folio (unnumbered), verso - cont. |
|
|
Anchor Signor Illustriſsimo calculando trouai la proportion, dil creſcere e calar che fa ogni pezzo de artegliaria (nelli ſuoi tiri) alzandolo ouer arbaſſandolo ſopra il pian de l’orizonte, et ſimilmente trouai il modo di ſaper trouar la uarieta de detti tiri in cadaun pezzo ſi grande come piccolo mediante la notitia d’un tiro ſolo (domente che ſempre ſia egualmente cargato) Dapoi inueſtigai, la proportione et l’ordini di tiri del mortaro, et ſimilmente trouai il modo di ſaper inuiſtigare ſotto breuita la uarieta de detti tiri pur per mezzo d’un tiro ſolo. Oltra di questo con ragioni euidentiſſime conobbi qualmente un pezzo de artegliaria poſſeua per due diuerſe uie (ouer elleuationi) percottere in un medemo luoco, et trouai il modo di mandar tal coſa (accadendo) a eſſecutione (coſe non piu audite ne d’alcun’altro antico ne moderno cogitate) Ma dapoi conſiderai (Signor Magnifico) che tutte queste coſe erano di puoco giouamento a un bombardiero quando che la diſtantia dil luoco doue gli occoreſſe di battere non gli fuſſe nota. Eſſempi gratia occorrendogli a tirare in un luoco apparente che la distantia di quello gli fuſſe occulta Che gli giouaria (O Magnanimo Duca) in questo caſo che lui ſapeſſe che il ſuo pezzo tiraſſe alla tal elleuatione paſſa 1356 et alla tal altra paſſa 1468, et alla tal altra paſſa 1574 et coſi diſcorrendo de grado in grado, certo nulla li giouaria, perche non ſapendo la distantia |
Moreover, Most Illustrious Lord, I found by means of calculations the proportion according to which the [ranges of] the shots of each piece of artillery increase and decrease when the piece is elevated or lowered above the plane of the horizon. Similarly,17 I also found the method of how to ascertain18 the characteristics of the mentioned shots in each piece, both large and small, solely on the basis of the information concerning one single shot (provided the piece is always charged in the same manner). Then,19 I investigated the proportions and characteristics of the shots of the mortar and, similarly, I found the method of how to ascertain the characteristics of the mentioned shots in a short time on the basis of the information concerning one single shot. Besides this, I found with a very evident argument that a piece of artillery can hit one place along two different paths (or at two different elevations) and I found the method of how to execute this in reality (a subject never heard20 or conceived by anyone else, ancient or modern). But then I realized that all these subjects (Magnificent Lord) are not really useful to the bombardier if he does not know the distance to the place he needs to strike. For example, if he needs to shoot at a place at a distance that is unknown, how could he make use (Magnanimous Duke) of the knowledge that allows him to shoot at 1356 steps if his piece is set at a certain elevation, or at 1468 steps at another elevation, or at 1574 at another elevation again, and so on, degree upon degree? It would not be at all useful because, unless he knows the distance, he will |
|
EPISTOLA - Quarto folio (non numerato), recto |
EPISTLE - Fourth folio (unnumbered), recto |
|
|
manco ſapra a che ſegno, ouer elleuatione debba aſſettar tal ſuo pezzo de artegliaria che percotta nel deſiderato loco, Seguita adonque due eſſer le principal parti neceſſarie a un real bombardiero (uolendo tirar con ragione et non a caſo) delle quale l’una ſenza l’altra quaſi niente gioua (Dico nelli tiri lontani) La prima è che groſſo modo ſappia conoſcere et inuestigare (con l’aſpetto) la distantia dil luoco doue gli occorre de tirare. La ſeconda è che ſappia la quantita di tiri della ſua artegliaria, ſecondo le ſue uarie elleuationi, le qual coſe ſapendo non errara de molto nelli ſuoi tiri ma mancandoui una di quelle non puo tirar (in conto alcuno) con ragione ma ſolamemte a diſcretione et ſe per caſo percotte al primo colpo nel luoco, ouer apreſſo al luoco doue deſidera, è piu presto per ſorte che per ſcientia (dico pur nelli tiri lontani) Perilche (Signor Illuſtrißimo) trouai un nouo modo da inuestigar ſotto breuita le altezze, profondità, larghezze, diſtantie ypothumiſſale, ouer diametrale, et ancora le orizontale delle coſe apparente, non in tutto come coſa noua, Perche in uero Euclide nella ſua perſpettiua ſotto breuita theoricamente in parte ne linſegna, ſimilmemte Giouanne Stoflerino, Orontio, Pietro Lombardo. et molti altri hanno datto a tal materie norma, chi con il ſole, chi con un ſpecchio, chi con il quadrante, chi con lo astrolabio, chi con due uirgule, chi con un baſtone (intitolato baculo de Iacob) et in molti altri uarij modi, Ma io dico (Signor Clarißimo) che trouai un nouo modo iſpidiente e preſto et facile da capire a cadauno (et a men errori ſuggetto de qualunque altro) da inuestigare le dette distantie, il quale da niun altro è ſtato poſto maßime delle diſtantie ypothumiſſale ouer diametrale ancora delle orizontale, le quale inuero ſono le piu neceſſarie al bombardiero de tutte le altre ſorte di dimenſioni, perche a quello non è molto neceſſario a ſapere la altezza duna coſa perpendicolarmente elleuata ſopra al orizonte, ne anchora la profondita duna coſa profunda, ne anchora la larghezza duna coſa lata, Ma ſolamente le dette distantie ypothumiſſale, et orizontale gli ſono molto al propoſito, come nel quarto libro (a uostra Illustrißima Signoria) ſi fara manifesto. |
not know at which point or elevation he has to set his piece of artillery so as to strike the place he desires. Therefore there are two21 fundamental subjects necessary to the real bombardier (if he does not want to shoot casually, but with cognition) and one subject without the other is not really useful (I say this concerning long shots).22 The first thing is that he has to be able to find out and investigate (by sight) the distance to the place he needs to shoot.23 The second is that he needs to know the quantities24 of the shots of his artillery according to the various elevations. If he knows both of these subjects, he will not make any major mistakes while shooting, but if one of these subjects is missing, he cannot shoot with cognition in any way but subjectively, and if he casually strikes the place he would like to strike, or if he strikes close to that place, this would be through luck rather than science (I repeat that this concerns long shots). For this reason, Very Illustrious Lord, I found a new method to measure in a short time the heights, depths, widths,25 diametral distances, or hypotenuses, and also the horizontal [heights] of the perceptible objects, though it is not a completely new subject. Euclid briefly explains the theory of parts of this subject in his Perspective. Similarly, Giovanne Stoflerino,26 Orontio,27 Pietro Lombardo and many others have standardized this subject. Someone used the Sun, others a mirror, a quadrant, an astrolabe or two rods, someone also used a stick (called a Jacob’s staff) and many other means were also used. But I say (Most Illustrious Lord) that I have found a new and fast method, easily understandable to everyone (and less subject to mistakes than any other method), to measure the mentioned distances. This method has not been suggested by anyone else, especially concerning the diametral distances or hypotenuses and horizontal distances. These measurements are indeed more essential28 to the bombardier than any other kind of measurement, because to him it is not particularly useful to know the height of an object elevated perpendicularly to the horizon, the depth of a low object or the width of a wide object. Particularly useful to him are only the hypotenusal and horizontal distances, as will be manifested (to the Most Illustrious Lordship) in the fourth book. |
|
EPISTOLA - Quarto folio (non numerato), recto - cont. |
EPISTLE - Fourth folio (unnumbered), recto - cont. |
|
|
Oltra di queſto per curioſita, me meſſe a ſcorrere li uarij modi oſſeruato da noſtri antiqui Naturali, et anchor da moderni nelle compoſitioni de fuochi et fra naturali inueſtigai la natura di quelle gumme, bitumi, graſſi, olei, ſali, acque ſtillate, et altri ſimplici minerali, et non minerali dalla natura prodotti, et da l’arte fabricati, componenti quelli, et conſequentemente trouai il modo di componere molte altre uarie et diuerſe ſpecie de fuochi non ſolamente alla diffenſione de ogni murata terra utilißimi, ma anchora in molte altre occurrentie molto al propoſito. Per le qual coſe haueua deliberato de regolar l’arte de bombardieri, et tirarla a quella ſottilita, che fuſſe poßibile de tirare (mediante alcune particolar iſperientie) perche in uero (come dice Ariſtotile nel ſettimo della Phyſica teſto uigeſimo) dalla iſperientia di particolari pigliamo la ſcientia uniuerſale. Ma poi fra me penſando un giorno, mi parue coſe biaſmeuole, uituperoſa, e crudele, et degna di non puoca punitione apreſſo a Iddio, et alli huomini a uoler studiare di aſſotigliare tal eſſercitio dannoſo al proßimo, anzi destruttore della ſpecie humana, et maßime de Chriſtiani in lor continue guerre. Perilche non ſolamente poſpoſi totalmente il studio di tal materia et atteſi a ſtudiar in altro, ma anchor ſtrazai, et abruſciai ogni calculatione, et ſcrittura da me |
Besides this and out of curiosity, I began to read the various methods, observed by our ancient ancestors and also by the moderns, to compound fires. Among the natural [subjects] I investigated the nature of those gums, bitumens, greases, oils, salts, distilled waters and other simple and not simple minerals, of which the above-mentioned things are constituted and that are produced by nature and manufactured by art. Consequently, I found the way to compound many other and different kinds of fires that are very useful not only for defending fortified land, but also for many other occasions.29 I had deliberated regulating the art of the bombardiers and achieving the perfection that can be achieved (by means of certain particular experiments) because (as Aristotle says in the seventh [book] of Physics, twentieth text), we reach universal science through the experience of the particulars. One day, however, I was thinking to myself30 and it seemed to me that working toward the perfection of such an art, harmful to the neighbor or even destructive for the human species and especially for the Christians because of their continuous wars, was a reproachful, vituperative and cruel thing, worthy of heavy punishment by God and by human beings.31 For this reason,32 not only did I completely postpone the investigation of such matters and begin to work on another subject, I also shredded and burned all the calculations and writings that I had |
|
EPISTOLA - Quarto folio (non numerato), verso |
EPISTLE - Fourth folio (unnumbered), verso |
|
|
notata, che di tal materia parlaſſe. Et molto mi dolſl, et auergognai del tempo circa a tal coſa ſpeſſo, et quelle particolarita, che nella memoria mi restorno (contra mia uolunta) iſcritte mai ho uoluto paleſarle ad alcuno, ne per amicitia, ne per premio (quantunque ſia ſtato da molti richieſto) perche inſignandole mi parea di far naufragio, e grande errore. Ma hor uedendo il luppo deſideroſo de intrar nel noſtro armento, et accordato inſieme alla diffeſa ogni noſtro pastore non mi par licito al preſente di tenere tal coſe occulte, anci ho deliberato di publicarle parte in ſcritto, et parte uiua uoce a ogni christiano, accioche cadauno ſia meglio atto ſi nel offendere, come nel diffenderſi da quello. Et molto mi doglio uedendo il biſogno che tal studio all’ora abandonai, perche ſon certo che hauendo ſeguito fin hora harei trouato coſe di maggior ualore come ſpero in breue anchora di trouare. Ma perche il preſente è ſcerto (e al tempo breue) il futuro è dubioſo uoglio iſpedire prima quello che al presente mi trouo, et per mandar tal coſa imparte a eſſecutione ho composto impreßia la preſente operina la quale ſi come ogni fiume naturalmente cerca di accoſtarſe, et unirſe col mare, coſi eſſa [(]conoſcendo uoſtra Illust. D. S. eſſer la ſomma fra mortali de ogni bellica uirtu) recerca di accostarſe, et unirſe con eſſa amplitudine. Pero ſi come lo abondante mare, il quale non ha di acqua biſogno non ſe ſdegna di receuer un picol fiume, coſi ſpero che uoſtra D. S. non ſe ſdegnara di acettarla, accioche li peritiſſimi bombardieri di questo noſtro Illuſtriſſimo Dominio ſugetti a uoſtra Sublimita, oltra il ſuo ottimo, et pratical ingegno, ſiano meglio di ragion iſtrutti, et atti a eſſeguire li mandati di quella. Et ſe in queſti tre libri non ſatisfaccio plenariamente uostra Eccellentiſſima Signoria inſieme con li predetti ſuoi peretiſſimi bombardieri, ſpero in breue con la pratica del quarto et quinto libro non gia in stampa (per piu riſpetti) ma ben a pena, ouer uiua uoce di ſadisfar in parte uoſtra Sublimita inſieme con quegli alla cui gratia da Infimo, et humiliſſimo Seruitore Diuotamente mi raccomando. Data in Venetia in le caſe noue di San Saluatore alli XX di Decembrio MDXXXVII. De uoſtra Illustriſſima D.S. Infimo Seruitore. Nicolo Tartaglia Briſciano. |
annotated concerning such matters. I was very upset and ashamed about the time I had spent [working on] this subject. Also, I did not want to tell anyone of those particular things that remained on my mind (against my will), neither because of friendship nor reward (though I was asked by many people to do so) and this was because, had I taught them, it seemed to me that I would be making a big mistake. But now, as I see the wolf33 wishing to join our flock and since each shepherd agrees with the need for defense, it does not seem licit to me to keep these things hidden and I have deliberated published them, partly in written form and partly viva voce with every Christian, so that everyone is better prepared to both attack [the wolf] and to defend himself. I now deeply regret34 abandoning such an investigation at that time, now that such knowledge is so necessary, and I am sure that had I continued I would have disclosed even more relevant subjects, as I hope to do in the near future. However, as the present is certain35 and the future is uncertain, I want to make public first what I have at disposal now. To realize this idea, at least partially, I quickly prepared the present short work. Just as all rivers tend naturally to get closer and join the sea, this short work tries to get closer and join You, as Your Illustrious Ducal Lordship is the sum, among mortals, of every virtue of war. Therefore, like the abundant sea that, though it needs no more water, nevertheless does not disdain from accepting a small river, I hope that Your Ducal Lordship does not disdain from accepting this work. In this way, the very skilled bombardiers of this our very illustrious Dominion, subject to Your Sublimity, besides being instructed by Your excellent and practical wisdom, will be better instructed also by the intellect and thus, better able to execute your orders. If, by means of these three books, I do not entirely satisfy Your Most Excellent Lordship and your mentioned very skilled bombardiers, I do hope that I will partly satisfy Your Sublimity and the others with the instructions contained in the fourth and fifth book, which are not yet in print (because of several reasons) but only handwritten, or by viva voce. As a small and humble servant, I devotedly recommend myself to You. Delivered in Venice at the new house of San Salvatore on the 20th of December 1537. Lowest Servant of Your Most Illustrious Ducal Lordship. Nicolo Tartaglia from Brescia. |
|
LIBRO PRIMO - 1r |
FIRST BOOK - 1r |
|
|
First Book COMINCIA IL PRIMO LIBRO DELLA NOVA SCIENTIA DI NICOLO TARTAGLIA BRISCIANO, dalle diffinitioni, ouer dalle deſcriptioni delli principij, per ſe noti delle coſe premeſſe. DIFFINITIONE PRIMA. Corpo egualmente graue è detto quello, che ſecondo la grauita della materia, et la figura di quella è atto à non patire ſenſibilmente la oppoſition di l’aere in alcun ſuo moto. OGNI corpo (come uoleno li naturali) ò che egli ſemplice ò che egliè compoſto, li ſemplici ſono cinque, cioe, terra, acqua, aere, fuoco, et cielo. Tutti li altri dicono eſſer compoſiti dalli preditti, et queſti tali ſono li huomini, li animali, le piante, le pietre, li ſette mettalli. Et ogni altra ſpecie di corpo. Delli detti cinque corpi ſemplici, quattro ſono detti elementali, cioè la terra, lacqua, laere, e il fuoco, Laltro è chiamato quinta eſſentia, cioè il cielo. Delli detti quattro elementali (come uol Auicena in la ſeconda dottrina della prima fen del ſuo primo libro) dui ſono leui et dui graui. Li leui ſono il fuoco e laere. Li graui ſono la terra, et lacqua, ma Auerrois ſopra il quarto de celo et mundo (teſte 29) uol che tutti li detti corpi in li ſuoi luochi habbino alcuna grauita, eccetto che il fuoco, etiam alcuna leuita eccetto che la terra. Onde ſeguiria che laere nel proprio luoco participaſſe de grauita. Per ilche ſeguita che ogni corpo compoſto di 4 elementi in aere participa de grauita. Niente di meno per corpo egualmente graue in queſto luoco ſe intende ſolamente quello che ſecondo la grauita de la materia, et la forma di quella è atto a non patire ſenſibilmente la oppoſitione de laere in alcun ſuo moto. Secondo la materia, cioè che ſia di ferro, ouer di piombo, ouer di pietra, ouer di altra materia ſimile in grauita. Secondo la forma, cioe ch’l ſia unito di tal qualita, ch’l ſia atto a non patire ſenſibilmente (per uigor della forma) la detta oppoſition de l’aere in alcun ſuo moto. Onde fra le figure, ouer forme de corpi, la forma Cunea, ouer Pyramidale ſaria la prima, che ſaria piu atta a temere meno la detta oppoſition de laere de qual ſi uoglia altra forma, domente che con arte la fuſſe conſeruata |
THE FIRST BOOK OF THE NEW SCIENCE OF NICOLO TARTAGLIA FROM BRESCIA STARTS with the definitions, the descriptions of the principles, [which are] self evident as premises. FIRST DEFINITION. An equally heavy body is said to be a body which, according to the heaviness and shape of the matter, is not perceptibly influenced by air opposition during its motion. All bodies, as the Naturals say, are either simple or compounded. The simple bodies are five, that is, earth, water, air, fire and sky. All other bodies are said to be compounded of the mentioned simple ones. The compounded ones are humans, animals, plants, stones, the seven metals and every other kind of body. Four of the mentioned five simple bodies are said to be elementary, that is, earth, water, air and fire. The other body is called the fifth essence, that is, the sky. Of the four elementary elements (as is said by Avicenna in the second doctrine of the first Fen36 of his first book) two are light and two are heavy. The light ones are fire and air. The heavy ones are earth and water. However, in the fourth [book] of De caelo et mundo (text twenty-nine), Averroes states that all the mentioned bodies have in their places37 a certain gravity, except for fire, and a certain levity, except for earth. Consequently, air in its place has a certain gravity. From this follows that each body, compounded of four elements, one of which is air, shares gravity.38 Nevertheless, an equally heavy body is univocally understood in this work as the body that, in reference to the heaviness and shape of its matter, is not perceptibly influenced in each of its motions by the opposition of the air. Concerning the matter, [it can be] of iron, of lead, of stone or of another material similar in reference to its heaviness. Concerning the shape, this is characterized by such a quality that makes it appropriate to not be influenced (because of its shape) by the opposition of the air during all of its motions. Therefore, among the figures and shapes of the bodies, the wedge-shaped object, that is the pyramidal shape, is the most appropriate among all possible shapes in order [for it] not to be influenced by the mentioned air, provided that by means of a contrivance the body would remain |
|
LIBRO PRIMO - 1v |
FIRST BOOK - 1v |
|
|
che la uertice, ouer acutezza di quella ſempre procedeſſe auanti contra limpeto del detto aere. Ma per che ſe la non fuſſe conſeruata, come è detto, non ſegueria il propoſito, per non eſſer egualmente graue, Poremo la figura ouer forma ſpherica ſenzaltra conditione eſſer la piu atta a patire meno la detta oppoſitione de l’aere in ogni ſpecie di moto di qual ſi uoglia altra forma per eſſer piu agile al moto da tutte le bande, et egualmente graue de qual ſi uoglia altra. Diffinitione. II. Li corpi egualmente graui ſono detti ſimili et eguali quando che in quegli non é alcuna ſuſtantial ne accidental differentia. Diffinitione. III. Lo inſtante e quello che non ha parte. Lo inſtate in el tempo e in el moto e ſi come il ponto geometrico in le magnitudine, cioe chel non ha parte ma e indiuiſibile et conſequentemente non e tempo ne anchora mouimento, ma ben e principio e fine de ogni tempo, et dogni mouimento terminato. Et e proprio l’ultimo fine del tempo preterito, et non e parte del tempo futuro. Et è principio del tempo futuro et non è parte del tempo preterito come Ariſ. nel 6 della Phyſi. (teſto 24) ci manifeſta. Diffinitione. IIII. Il Tempo e una miſura del mouimento, et della quiete, li termini del quale ſon dui iſtanti. IL tempo da ſcientifici è ſtato in diuerſi modi diffinito, cioe alcuni dicono (come hauemo detto diſopra) que’leſſer una miſura del mouimento, Et della quiete. Altri determinan eſſer inducia del moto delle coſe uariabile. Alcuni conchiudano eſſer uiciſſitudine de coſe: le quale in molti modi per ſottil indagatione ſe cognoſcono. |
in a position so that its top would always proceed while remaining in front against the impetus of the mentioned air. If the object does not retain such a position, as has been said, it would not work properly as it would not be equally heavy.39 Without further investigation, we define the spherical figure or shape as the most appropriate among all possible shapes in order to avoid the mentioned opposition of the air in the frame of each kind of motion. This [spherical] shape is most appropriate for the motion on all of its sides and it is equally heavy on all of its sides as well. Second definition. Equally heavy bodies are said to be similar and equal when they do not show [among each other] any substantial or accidental differences. Third definition. The instant is that which does not have parts. The instant of time and of motion is like the geometrical point in the frame of magnitudes. It does not have parts and it is indivisible. Consequently, it is neither time nor motion but the beginning and end of each time and motion that are finite. It is the last end of the past time and this is not part of the future time. It is the beginning of the future time and this is not part of the past time, as Aristotle shows us in the sixth [book] of Physics (text twenty-four). Fourth definition. Time is a measure of motion and of the state of rest; its ends are two instants. Time has been defined by the scientific fellows in different ways. Certain [persons] say, as we have said above, that time is a measure of movement and rest. Others say it is the end of the motion of things that vary. Others conclude that it is the vicissitude of things and [such vicissitude] can be known in many ways by means of acute investigation. |
|
LIBRO PRIMO - 1v - cont. |
FIRST BOOK - 1v - cont. |
|
|
Et altri dicono eſſer una eta uolubile che preſto manca. Delle quali diffinitioni hauemo tolto la prima per eſſer piu accomodata al noſtro propoſito. Digando che il tempo è una miſura del mouimento, et della quiete: perche ſi come per mezzo de una miſura materiale (in piu terre chiamata perticha diuiſa in piedi 6. Et ciaſcun pie in once 12) ſe uiene in cognitione della longhezza, larghezza, et altezza di corpi materiali. Similmente per mezzo de una miſura di tempi (chiamata anno diuiſo in meſi 12 e ciaſcun meſe comunamente in giorni 30 e ciaſcun giorno in hore 24 e ciaſcuna hora in minuti 60) ſe conoſce la differentia di moti de corpi; cioe la uelocita. et tardita de quelli. Perche ſe conoſciuto in le ſette ſtelle erratice una eſſer di moto piu ueloce de l’altra? Se non per la miſura de eſſi mouimenti chiamata anno |
Others say it is an inconstant age that is soon missed. We have chosen the first of these definitions because it is more appropriate for our purpose. In the same way as the length, width and height of the material bodies can be known by means of a material unity of measurement (which is called perch in many countries and is divided into six feet and each foot into twelve inches), it is said that time is the measure of movement and of quiet. Similarly, by means of a unity of measurement for time (which is called year, divided into twelve months, and each month commonly [divided] into thirty days, each day into twenty-four hours and each hour into sixty minutes), the differences of the motions of the bodies can be known, that is, their velocity and slowness. How could it be known that one of the seven erratic stars has a faster motion than the others? By means of the measurement of their movements which is called year |
|
PRIMO LIBRO - 2r |
FIRST BOOK - 2r |
|
|
con le ſue parti (cioe meſi giorni hore e minuti) come chiaro appare in le determinationi Aſtronomatice. Et li termini di queſto anno, cioe il principio e fin di quello ſono dui iſtanti, il medemo ſi deue intendere in le altre ſue parti et in ogni altro tempo terminato. Diffinitione. V. Il mouimento dun corpo egualmente graue e quella tranſmutatione, che alle uolte fa da uno loco a un altro, li termini dil qual ſon dui iſtanti. Il mouimento da tutti li ſcientifici e maſſime da Ariſtotile nel quinto della Phyſica (teſto 9) è ſtato diffinito eſſer una mutatione, ouer traſmutatione. Ma le ſpecie di queſto mouimento, ouer traſmutatione alcuni uoleno che ſiano 6 cioe Generatione, Corrottione, Augmentatione, Diminutione, Alteratione, et mutation di luoco. Ma Ariſtotile in lo preallegato loco uole che le mutationi ſiano 3 e non piu, cioe mutation de quantita: de qualita, et ſecondo il luoco. Delle qual ſpecie hauemo tolto ſolamente la ultima (perche le altre non fanno al propoſito) dicendo, che il mouimento dun corpo egualmente graue e quella traſmutatione, che alle uolte fa da un luoco a uno altro, come ſaria a dir di ſuſo in giuſo, et di giuſo in ſuſo, di qua e di la dal’a banda deſtra alla ſiniſira et e conuerſo. Et li termini de tali mouimenti (cioe in principio e fin di quelli[)] ſono dui iſtanti. Diffinitione. VI. Mouimento naturale di corpi egualmente graui e quello che naturalmente fanno da un luogo ſuperiore a un’altro inferiore perpendicularmente ſenza uiolenza alcuna. Diffinitione. VII. Mouimento uiolente di corpi egualmente graui e quello che fanno sforzatamente di giuſo in ſuſo, di ſuſo in giuſo, di qua et di la, per cauſa di alcuna poſſanza mouente. Diffinitione. VIII. Li mouimenti de corpi egualmente graui, ſe dicono eguali quando che li detti corpi ſon ſimili, et uanno de egual uelocita |
with its parts (that is months, days, hours and minutes) as it clearly appears in the astronomical40 investigations. The ends of such a year, that is its beginning and end, are two instants. The same is true for all other parts of it and for all finite times. Fifth definition. The movement of an equally heavy body is the transmutation that it sometimes accomplishes from one place to the other, whose ends are two instants. All the scientific fellows and especially Aristotle in the fifth [book] of Physics (text nine) have defined movement as a mutation, that is, a transmutation. Someone counts six kinds of movements or transmutations: generation, corruption, augmentation, diminution, alteration and mutation of place. Aristotle, however, in the mentioned place defines the mutations as three and not one more: mutation of quantity, of quality and of place. From these sorts here we use only the last (because the others are not useful for our purpose) and we say that the movement of an equally heavy body is the transmutation, that it sometimes makes from one place to the other, as for instance downwards, upwards, from right to left and vice-versa. The end of such movements (that is their beginnings and their ends[)] are two instants. Sixth definition. The natural movement of equally heavy bodies is the movement they accomplish from a higher place to a lower one, perpendicularly and without any violence. Seventh definition. The violent movement of equally heavy bodies is the movement they accomplish with effort either upwards or downwards, to the right or the left, and is caused by a moving power. Eighth definition. The movements of equally heavy bodies are said to be equal when the mentioned bodies are similar and move with the same velocity, |
|
LIBRO PRIMO - 2v |
FIRST BOOK - 2v |
|
|
cioe che in tempi eguali tranſiſcono interualli eguali. Diffinitione. IX. Reſiſtente ſe chiama qualunque corpo manente, che per far reſiſtentia a un corpo egualmente graue in alcun ſuo moto uien da quello offeſo. Diffinitione. X. Reſiſtenti ſimili, ſe dicono quelli corpi, che reſtariano egualmente offeſi, da corpi ſimili egualmente graui, in mouimenti eguali, et in mouimenti ineguali inegualmente offeſi, cioè che quello, che faceſſe reſiſtentia al piu ueloce reſtaſſe piu offeſo. Diffinitione. XI. Lo effetto dun corpo egualmente graue ſe dice la offenſione, ouer percußione, ouer il bucco che in ogni moto cauſa in un reſiſtente. Diffinitione XII. Et quando le percussioni, ouer bucchi de corpi ſimili egualmente graui, ſono eguali, ſe dicono effetti eguali, et ſe ineguali, ineguali effetti. Diffinitione. XIII. Poſſanza mouente uien detta qualunque artificial machina, ouer materia, che ſia atta a ſpingere, ouer tirare un corpo egualmente graue uiolentemente per aere. Diffinitione. XIV. Le poſſanze mouente, uengono dette ſimile et eguale quando che in quelle non é alcuna ſuſtantia ne accidental differentia nel ſpinger de corpi egualmente graui ſimili et eguali, |
that is, they move along equal intervals in equal times. Ninth definition. A body that is at rest and opposes resistance to an equally heavy body during its motion and is damaged by the latter is called resistant. Tenth definition. Those bodies that are damaged in the same way by similar equally heavy bodies during equal movements are called similar resistants. If the movements are unequal, they are unequally damaged so that the body that is damaged by the faster one is damaged more. Eleventh definition. The effect of an equally heavy body is called damage or percussion or the hole that is caused in each resistant during each motion. Twelfth definition. When the percussions or holes of similar equally heavy bodies are equal, the effects are said to be equal. If they are unequal, the effects are unequal. Thirteenth definition. The moving power is said to be any artificial machine or matter that is able to push or throw an equally heavy body violently through the air. Fourteenth definition. The moving powers are said to be similar and equal when there is no substantial or accidental difference [in their motions] while pushing equally heavy bodies which are similar and equal. |
|
LIBRO PRIMO - 3r |
FIRST BOOK - 3r |
|
|
Ma quando in quelle e alcuna accidental differentia ſono dette dißimile, et ineguale. Suppoſitione prima. El ſe ſuppone che il corpo egualmente graue (in ogni mouimento) uada piu ueloce doue fa, ouer faria (per comuna ſententia) maggior effetto in un reſiſtente. Suppoſitione. II. El ſe ſuppone che dui corpi egualmente graui ſimili et eguali, habbino tranſito, ouer che trapaſſeranno in tempi eguali ſpacij eguali terminanti in dui iſtanti, doue detti corpi paſſerebbono di egual uelocita. Suppoſitione. III. Et ſe ſuppone doue che corpi egualmente graui ſimili et eguali, fariano (per commune ſententia) eguali effetti in reſiſtenti ſimili, paſſerebbono per tai iſtanti, ouer luochi de egual uelocita. Suppoſitione. IIII. Ma doue fariano ineguali effetti ſe ſuppone, che quelli paſſerebbono de ineguali uelocita, et che quello, che faria maggior effetto paſſeria piu ueloce. Suppoſitione V. Li effetti de corpi egualmente graui ſimili et eguali fatti nelli ultimi iſtanti di lor moti uiolenti in reſiſtenti ſimili |
But if there is some substantial or accidental difference they are called dissimilar and unequal. First supposition. It is supposed that an equally heavy body (during each motion) moves faster when it produces or would produce (for common judgement) a greater effect against a resistant. Second supposition. It is supposed that two equally heavy bodies similar and equal to each other have the [same] transit, that is, they cover equal spaces in equal times that end with two instants, if the mentioned bodies move with the same velocity. Third supposition. It is supposed that if two equal and similar equally heavy bodies produce (for common judgement) equal effects in similar resistants, they go through the same instants, that is, places with the same velocity. Fourth supposition. But if they produce unequal effects, it is supposed that they go through unequal velocities and the one that produces the greater effect goes through faster. Fifth supposition. The effects produced in similar resistants by equally heavy bodies, which are equal and similar to each other during the last instants of their violent motions, |
|
LIBRO PRIMO - 3v |
FIRST BOOK - 3v |
|
|
ſe ſuppongono eſſer eguali. Comune ſententie. Prima Quanto piu un corpo egualmente graue uera da grande altezza di moto naturale, tanto maggior effetto fara in un reſiſtente. Seconda. Se corpi egualmente graui ſimili et eguali ueranno da egual altezza ſopra a reſiſtenti ſimili di moto naturale faranno in quegli eguali effetti. Terza. Ma ſe uerranno da ineguale altezza, faranno in quegli ineguali effetti, et quello che uera da maggior altezza fara maggior effetto. Ma biſogna notare che le dette altezze ſi deueno intendere reſpetto alli reſiſtenti. Quarta. Se un corpo egualmente graue nel moto uiolento trouara alcun reſiſtente, quanto piu el detto reſiſtente ſara propinquo al principio di tal moto, tanto maggior effetto fara il detto corpo in lui. Propoſitione. Prima. Ogni corpo egualmente graue nel moto naturale, quanto piu el ſe andara aluntanando dal ſuo principio, ouer appropinquando al ſuo fine, tanto piu andara veloce. |
are supposed to be equal. First common sentence.41 The greater the height from which an equally heavy body descends in natural motion, the greater the effect it produces on a resistant.42 Second [common sentence]. If equally heavy bodies, similar and equal to each other, descend from an equal height on similar resistants in natural motion, they produce equal effects on them. Third [common sentence]. But, if they descend from unequal heights, they produce unequal effects and the one that descends from a greater height produces a greater effect. One has to note, however, that the mentioned heights have to be conceived in respect of [the position] of the resistants. Fourth [common sentence]. If an equally heavy body finds a resistant along its violent motion, the closer the resistant is to the beginning of the motion, the greater the effect is that the mentioned body produces on it. First proposition. The farther each equally heavy body goes along its natural motion from its beginning, or the closer it comes to its end, the faster it travels. |
|
LIBRO PRIMO - 4r |
FIRST BOOK - 4r |
|
|
Esſempio ſel fuſſe le 3 diuerſe altezze A B C in retta linea, come di ſotto appare, et che dalla altezza A per caſo caſcaſſe da ſe vn corpo egualmente graue, ſenza dubbio quello tal corpo, non trouando reſiſtentia andaria di moto naturale ſin in terra facendo il viazzo ſuo alla ſimilitudine de la linea DEFG hor dico che il moviment[o] di quello tal corpo ſaria di tal conditione che quanto piu el ſe andaſſe aluntanando dal ſuo principio (cioe da lo iſtante, ouer ponto D) ouer appropinquando al ſuo fine (cioe allo iſtante, ouer ponto G[)] tanto piu andaria ueloce. Perche il detto corpo in tal mouimento (per la prima comuna ſententia) faria maggior effetto in vn reſiſtente, il qual fuſſe fuor dalla altezza A43 che dalla altezza B. Seguitaria adunque, che il detto corpo (per la prima ſuppoſitione) andaria piu ueloce per lo ſpacio EF che per lo ſpacio DE. Similmente perche lo detto corpo (per la detta prima comuna ſententia) faria maggior effetto in un reſiſtente, che fuſſe nel ponto G, che ſel fuſſe alla altezza C. Seguiria adoncha (per la medema prima ſuppoſitione) che lo detto corpo andaria piu veloce per lo ſpacio FG che per lo ſpacio EF et ſe paſſar poteſſe il ponto G cioè che la terra gli andaſſe cedendo loco, como fa l’aere andaria continuamente augumentando in uelocita, fin al centro dil mondo poi in eſſo centro ſe ripoſaria (per comuna sententia de Philoſophi) ſi che quando lo detto corpo fuſſe propinquo al detto centro, ueria a eſſer di moto piu uelociſſimo, che in alcun paſſato ſpacio fuſſe stato che é il propoſito. Queſto medemo ſe uerifica ancora in cadauno che vada uerſo un loco deſiato che quanto piu ſe ua approßimando al deto loco, tanto piu ſe ua allegrando, e piu ſe sforza di caminare, como appar in un peregrino, che uenga dalcun luoco luntano che quando è propinquo al ſuo paeſe, ſe sforza naturalmente al caminar a piu potere tanto piu quanto piu uien di lontan paeſi pero il corpo graue fa il medemo andando uerſo il ſuo proprio nido, che è il centro dil mondo, et quando piu vien di lontano in eſſo centro, tanto piu (giongendo a quello) andaria veloce. ANcor che la opinione de molti ſia che ſel fuſſe un forame che penetraſſe diametralmente tutta la terra, et che per quello fuſſe laſſato andar un corpo egualmente graue, come diſopra e ſtato detto, che quel tal corpo gionto che fuſſe al centro del mondo immediate iui ſe fermaria, la qual openione, dico non eſſer uera che coſi immediate che ui fuſſe agionto ui ſe gli fermaſſe, |
For example, let there be three different heights A, B, C along a straight line, as it appears below. Casually, an equally heavy body falls down from the height A. That body, as it does not find any resistance, certainly moves along a natural motion down to the bottom and travels in a way similar to the line DEFG. I say that the movement of that body has that characteristic according to which the farther it moves away from its beginning (that is, from the instant or point D), or the closer it comes to its end (that is, to the instant or point G[)], the faster it goes. This occurs because the mentioned body that moves with such a motion (because of the first common sentence) produces a greater effect on a resistant if it falls from height A44 than from height B. It follows from the foregoing that the mentioned body45 (because of the first supposition) travels faster along space EF than along space DE. Similarly, as the mentioned body (because of the mentioned first sentence) produces a greater effect on a resistant at point G than if it were at [the point of] height C, it follows that (because of the same first supposition) the mentioned body travels faster along space FG than along space EF. If it could then travel beyond point G, that is, if the earth gave free space to it as the air does, it would continuously increase its velocity until [it reaches] the center of the Earth. Then it would rest at that center (according to the common judgement of the Philosophers). Thus, when the mentioned body is close to the mentioned center, it has [reached] a faster motion than in any other space through which it has traveled before, which was to be demonstrated. The same happens each time one moves toward the place that one aspires to, and the closer one comes to that place, the happier one is and the more effort one puts into walking fast. It appears to be similar for the pilgrim who comes from a distant place and who is approaching his village. The closer he gets, the greater effort he naturally makes to walk in the fastest way possible, and the faster he goes, the more distant the place is from which he came. The heavy body behaves in the same way when it moves toward its nest, that is, the center of the world: the farther it moves from that center from which it came, the faster it travels (the closer it gets to it).46 It is the opinion of many that if a hole diametrically penetrated the entire Earth and if an equally heavy body was allowed to travel through that hole, as has been said above, the mentioned body would immediately rest as soon as it reached the center of the world. I claim that the opinion that it would stop immediately when it arrived there is not true. |
|
LIBRO PRIMO - 4r - cont. |
FIRST BOOK - 4r - cont. |
|
|
anci per la grande uelocita che in quello ſi trouaſſe ſaria sforzato a paßare di moto uiolente molto, e molto oltra il detto centro ſcorendo uerſo il cielo del noſtro ſubterraneo emiſperio, da poi retornaria di moto naturale uerſo il medemo centro, et gionto a quello lo paßaria ancor per le medeſime ragioni di moto uiolente uerſo di noi, Et pur di nouo retornaria pur di moto naturale uerſo il medeſimo centro, et pur di nouo lo paßaria di moto uiolente, et da poi retornaria di moto naturale, et coſi andaria un tempo paſſando di moto uiolente, et ritornando di moto naturale ſminuendoſi continuamente in lui la uelocita, et finalmente ſe fermaria poi nel detto centro. Per il che egliè coſa manifeſta che dal moto naturale ſi cauſa il uiolente, et non è conuerſo, cioe che dal uiolente giamai uien cauſato il naturale, anci ſi cauſa per ſe. |
Because of the great velocity that it has at that [point], it would be forced to go through [the hole] according to its violent motion for longer and longer [space] beyond the mentioned center and toward the sky of the hemisphere beneath us. It would then move back along a natural motion toward the same center, and once it arrived would pass it again for the same reason, but along a violent motion toward us. And again it would move back along a natural motion toward the same center and again would pass it due to the violent motion. In this way, a certain time would elapse during which it would pass [the center] with its violent motion and then come back because of its natural motion, continuously decreasing its velocity and, finally, coming to rest at the mentioned center. Therefore, it is evident that the violent motion is caused by the natural one, but not the opposite. That is, the natural motion is never caused by the violent one. This is caused by itself. |
|
LIBRO PRIMO - 4v |
FIRST BOOK - 4v |
|
 Correlario Primo. Onde el ſi manifeſta ancora qualmente ogni corpo egualmente graue in el principio del mouimento naturale ua piu tardißimo, et in fin piu uelocißimo che in ogni altro luoco, et quanto piu paſſera per longo ſpacio tanto piu in fine andara uelocißimo. Correlario. II. Anchora è manifeſto qualmente un corpo egualmente graue di moto naturale non puo paſſare per dui diuerſi iſtanti |
 First corollary. It is therefore manifest that every equally heavy body travels slowest at the beginning of its natural motion and is faster at the end [of its motion] than at any other place, and the longer the space is that it has traveled, the faster it is at the end. Second corollary. It is also manifest that an equally heavy body [moving] with natural motion cannot pass through two different instants with |
|
LIBRO PRIMO - 5r |
FIRST BOOK - 5r |
|
|
di egual uelocita. Propoſitione. II. Tutti li corpi egualmente graui ſimili, et eguali dal principio delli lor mouimenti naturali, ſe partiranno de egual uelocita, ma giongendo al fine di tali lor mouimenti, quello che hauera paſſato per piu longo ſpacio andara piu ueloce. SEl fuſſe le quatro diuerſe altezze A, B et C, D poſte a due a due in retta linea come diſotto appare, et che la altezza A fuſſe tanto lontana dalla 
|
the same velocity. Second proposition. If all equally heavy bodies, similar and equal to each other at the beginning of their natural motions, start [moving] with the same velocity, when they arrive at the end of their movements, the one that has passed a longer space will have traveled faster. Let the four different heights A, B and C, D be placed in twos on a straight line as it appears below, and let height A be as far from 
|
|
LIBRO PRIMO - 5v |
FIRST BOOK - 5v |
|
|
altezza B quanto è la altezza C dalla altezza D et che per caſo dalla altezza A47 caſcaſſe un corpo egualmente graue, et un’altro ne caſcaſſe dall’altra altezza C li quai corpi fuſſeno ſimili, et eguali. Le noto che quegli tai corpi andariano di moto naturale in terra, et li tranſiti loro ſariano retti e perpendicolari alla terra cioe alla ſimilitudine delle due linee GF et IE. Hor dico che queſti tai corpi ſe partiriano dal ſuo principio (cioe l’uno dallo iſtante, ouer ponto G et l’altro dallo iſtante ouer ponto I) de egual uelocita, ma giongendo al fine di tali mouimenti, cioe alli dui iſtanti E et F quello che ueniſſe dalla altezza A andaria piu veloce di l’altro perche quello haueria tra[n]ſito per piu longo ſpacio el quale è il ſpacio AF. Perche l’altezza B é tanto lontana dalla altezza A quanto che è l’altezza D dall’altezza C (dal proſupoſito) adonque il corpo: che cadeße dalla altezza A percottendo in uno reſiſtente, che fuße fuora dalla altezza B el non faria in quello maggior effetto (per la ſeconda comuna ſententia) di quello che faria quello, chi cadeße dalla altezza C ſopra dun’altro ſimile che fuße fuora della altezza d[’]onde (per la terza ſuppoſitione) li detti dui corpi andaranno l’uno per l’altezza B in ponto H et l’altro per l’altezza D in ponto K de egual uelocita. dil che (per la ſeconda ſuppoſitione) li detti dui corpi andarrano l’uno il ſpacio GH et l’altro il ſpacio IK in tempi eguali. Adonque li detti dui corpi ſe partiriano dal principio de lor mouimenti (cioè l’uno da lo istante G et l’altro da lo iſtante I) de egual uelocita che é il primo propoſito. Et perche il corpo, che ueniße dall’altezza A faria maggior effetto in un reſiſtente, che fuße in lo iſtante F (per la terza comuna ſententia) di quello che faria quello che ueniße dalla altezza C in un’altro ſimile chi fuße in ponto E. Onde (per la prima ſuppoſitione) lo detto corpo che uerria dall’altezza A giongendo al fin dil ſuo mouimento (cioé allo iſtante, ouer ponto F) andaria piu ueloce di quello che uerria dall’altezza C giongendo al ſuo fine, cioè allo iſtante, ouer ponto E che è il ſecondo propoſito. A dimoſtrar el medemo ſecondo propoſito per un altro modo: de tutta la linea, ouer tranſito GF maggiore, ne tagliaremo (per la terza del primo de Euclide) la parte GM egual al tranſito, ouer linea IE minore et perche tutti li corpi egualmente graui ſimili, et eguali dal principio delli loro mouimenti naturali ſe parteno de egual uelocita (come di ſopra fu dimonstrato) lo corpo adonque che ſe parteße dall’altezza A andaria tanto ueloce per lo ſpacio GM quanto faria quello che ſe partiße dall’altezza C per lo ſpacio IE cioé ambi doi tranſiriano in tempi eguali. |
height B as height C is from height D. Let an equally heavy body casually fall from height A48 and another one from the other height C; these bodies are similar and equal [to each other]. I point to the fact that those bodies would move toward the ground with a natural motion and their transits would be straight and perpendicular to the ground, as lines GF and IE show. I claim that these two bodies start off from their beginning (that is, one from the instant or point G and the other from the instant or point I) with equal velocities. Then, when they come to the end of their movements, that is, at the two instants E and F, the one that comes from the height A moves faster than the other because it has transited a longer space, that is, the space AF. Since the height [of point] B is as far from the height [of point] A as the height [of point] D is from the height [of point] C (as has been supposed), the body that falls from height A, if it hits a resistant placed in front of height B, would not produce a greater effect (because of the second common sentence) than that produced by the [body] that falls from height C over a similar resistant placed in front of height D. Therefore (because of the third supposition), the mentioned two bodies travel at the same velocity when they pass the first [body] at height B, [that is,] at point H, and the other [body] at height D, [that is,] at point K. Consequently (because of the second supposition), the mentioned two bodies travel in equal times, one [through] the space GH and the other [through] the space IK. Therefore, the mentioned two bodies begin their movements (one at instant G and one at instant I) with equal velocity. Which was to be shown first. Since the body that comes from height A produces a greater effect on a resistant placed at instant F (because of the third common sentence) than the effect produced by the [body] that comes from height C on a similar resistant placed at point E, (because of the first supposition) the mentioned body coming from height A, when it arrives at the end of its movement (that is, at the instant or point F), moves faster than the [body] that comes from height C, and when it arrives at the end of its movement, that is, at the instant or point E. Which was to be shown secondly. This second point [of the argument] can be demonstrated also by means of another method. Of the entire longer line or transit GF, we take (because of the third [proposition] of the first [book] of Euclid) the part GM which is equal to the transit or shorter line IE. Since equally heavy bodies, similar and equal to each other, all begin their natural motions with the same velocity (as demonstrated above), the body that starts at height A travels along the space GM as fast as the body that starts at height C along the space IE, that is, they travel in equal times. |
|
LIBRO PRIMO - 5v - cont. |
FIRST BOOK - 5v - cont. |
|
|
Et perche lo detto corpo: che ſe partiße dall’altezza A (per la precedente propoſitione) andaria piu ueloce per lo ſpacio MF che per lo ſpacio GM (per comuna ſcientia) andaria anchora piu ueloce per lo detto ſpacio MF che l’altro per lo ſpacio IE che il medemo ſecondo propoſito. Propoſitione III. Quanto piu un corpo egualmente graue ſe andara luntanando dal ſuo principio, ouer propinquando al ſuo fine, nel |
Since the mentioned body that starts from height A (because of the previous proposition) travels faster along the space MF than along the space GM, (because of the common knowledge) it also travels faster along the mentioned space MF than along the other space IE, which is the same as the second point [of the argument]. Third proposition. The more an equally heavy body moves away from its beginning in a violent motion, that is, the closer it gets to its end, |
|
LIBRO PRIMO - 6r |
FIRST BOOK - 6r |
|
|
moto uiolente, tanto piu andara pigro e tardo. ESſempi gratia, ſel fuſſe una poßanza mouente in ponto A che tirare uoleße, ouer doueße un corpo egualmente graue uiolentemente per aere, et che tutto il tiro che far poteße, ouer doueße la detta poßanza con eßo corpo fuße tutta la linea AB. Dico che quello tal corpo quanto piu il ſe andaße aluntanando dal ſuo principio (cioè da lo iſtante A) ouer approßimando al ſuo fine (cioè allo istante B) tanto piu ſe andaria alentando de uelocita, la qual coſa ſe dimoſtrara in queſto modo. Diuideremo tutta la detta linea, ouer tranſito AB in piu ſpacij, et ſiano BC, CD, DE, EF, FG, GH et HA. Hor perche il detto corpo (per la quarta comuna ſententia) faria maggior effetto in un reſiſtente eßendo quello in ponto C che non faria eßendo in ponto B dilche 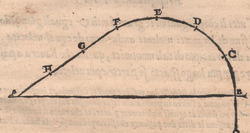 (per la prima ſuppoſitione) lo detto corpo andaria piu ueloce per lo ponto C che per lo ponto B et ſimilmente per lo ſpacio D[C] che per lo ſpacio CB coſi per le medeme raggioni lo detto corpo andaria piu ueloce per lo ſpacio ED che per lo ſpacio DC et per lo ſpacio FE che per lo ſpacio ED et per lo ſpacio GF che per lo ſpacio FE et per lo ſpacio HG che per lo ſpacio GF et per lo ſpacio AH49 che per lo ſpacio HG et ſe piu auanti fuße il principio di tal moto uiolente, tanto piu nelli ſeguenti ſpacii andaria ueloce, che è il propoſito. Questo medemo ſe ueriſica in cadauno che ſia uiolentemente menato uerſo a un luoco da eßo odiato: che quanto piu ſe ua approßimando al detto luoco, tanto piu ſe ua atriſtando in la mente, et piu cerca de andar tardigando. Correlario Primo. Onde el ſe manifeſta qualmente un corpo egualmente graue in lo principio d’ogni moto uiolente, ua piu uelocißimo, et |
the slower it travels. For example, let the moving power that wants or has to throw an equally heavy body violently through the air be at point A, and let the entire shot that the mentioned power could or should make be the entire line AB. I say that the farther away this body travels from its beginning (that is, from the instant A) or the closer it gets to the end (that is, to the instant B), the slower its velocity is, and this is demonstrated in the following way. We divide the entire mentioned line, or transit, AB into several spaces and these are BC, CD, DE, EF, FG, GH and HA. Now, since the mentioned body (because of the fourth common sentence) produces a greater effect on a resistant at point C than at point B, it follows  (because of the first supposition) that the mentioned body travels faster through point C than through point B and likewise through the space D[C]50 than through the space CB. Therefore, and for the same reasons, the mentioned body travels faster through the space ED than through the space DC, and through the space FE than through the space ED, and through the space GF than through the space FE, and through the space HG than through the space GF, and through the space AH51 than through the space HG. The farther away the beginning of the violent motion is, then likewise the faster it would travel in the previous spaces, which is to be shown. This same [effect] happens to everyone who has to go to an odious place: the closer he gets to that mentioned place, the sadder he becomes and the more he tries to slow down his journey. First Corollary. Hence, it is manifest that an equally heavy body travels fastest at the beginning of its violent motion and |
|
LIBRO PRIMO - 6v |
FIRST BOOK - 6v |
|
|
in fin piu tardisſimo che in ogni altro luoco, et quanto piu hauera a paſſare per piu longo ſpacio tanto piu in lo principio di tal mouimento andara uelocisſimo. Correlario. II. Anchor è manifeſto qualmente un corpo egualmente graue di moto uiolente non puo paſſare per dui diuerſi iſtanti de egual uelocita. Propoſitione. IIII. Tutti li corpi egualmente graui ſimili et eguali giongendo al fine de lor motti uiolenti andaranno de egual uelocita, ma dal principio di tali mouimenti, quella che hauera a paſſare per piu longo ſpacio ſe partira piu ueloce. ESfempi gratia ſel fuße due poßanze mouente dißimile, et ineguale luna in ponto A e l’altra in ponto C che tirar doueſſen dui corpi egualmente graui ſimili et eguali uiolentemente per aere, et che tutto il tiro: che far doueſſeno le ditte due poſſanze con eßi corpi l’uno fuße la linea AB et 
|
slower than in any other place at the end. The longer the space is to travel, the faster it is at the beginning of its movement. Second corollary. It is also manifest that an equally heavy body [that moves] with violent motion cannot travel through two different instants with the same velocity. Fourth proposition. All equally heavy bodies, similar and equal to each other, travel with the same velocity when they arrive at the end of their violent motions. But, at the beginning of such movements those [bodies] that travel along longer spaces start off faster. For example, let there be two different and unequal moving powers, one at point A and the other at point C, that have to throw two equally heavy bodies, similar and equal to each other, violently through the air, and let the entire shots that the mentioned two powers realize with the mentioned bodies be line AB the first and 
|
|
LIBRO PRIMO - 7r |
FIRST BOOK - 7r |
|
|
l’altro la linea CD. Dico che queſti dui corpi giongendo al fine di queſti dui lor mouimenti uiolenti, cioe l’uno allo iſtante, ouer ponto B et l’altro allo istante, ouer ponto D andariano de egual velocita. Ma dal principio di tali loro mouimenti cioe, l’uno da lo iſtante A et l’altro da lo iſtante C ſe partiriano de inegual uelocita, perche quello che doueria paßare per lo tranſito, ouer ſpacio AB (per eſſer piu longo di l’altro) ſe partira piu veloce da lo iſtante A che non fara l’altro da lo iſtante C la qual coſa ſe dimoſtrara in queſto modo. Perche ſe li detti dui corpi trouaßeno alcun reſiſtente in li dui iſtanti D et B li quali fußeno ſimili et eguali in reſistentia. fariano in eßi dui effetti (per la quinta ſuppoſitione) eguali onde (per la tertia ſuppoſitione) andariano de egual uelocita, che è il primo propoſito. A dimonstrar il ſecondo dal tranſito, ouer linea AB maggiore ne ſegaremo con la imaginatione la parte BK egual al tranſito, ouer linea CD, minore, et perche li detti dui corpi giongendo alli dui iſtanti D et B andariano de egual uelocita (come di ſopra è ſta dimoſtrato) haueriano tranſito de egual uelocita ſpacij egualmente distanti da li preditti dui lochi, ouer iſtanti B et D (per la ſeconda ſuppofitione) Adonca li detti dui corpi tranſiriano de egual uelocita l’uno per lo ſpacio KB partiale, et l’altra per lo ſpacio CD totale, cioè. Paßariano quegli in tempi eguali. Et perche quanto piu un corpo graue (nel moto uiolente) ſe andara aluntanando dal ſuo principio (per la terza propoſitione) tanto piu andara pigro e tardo. Adonque il corpo che ueniße da lo iſtante A andaria piu veloce per lo ſpacio AK che per alcun luoco del ſpacio KB partiale, ſeguita adonca (per comuna ſcientia) che il corpo che ueniße dallo istante A andaria piu ueloce per lo ſpacio AK che non andaria l’altro in alcun luoco di ſpacio CD totale. Il corpo adonque, che ueniſſe dal ponto, ouer istante A ſi parteria piu ueloce da eßo iſtante A, che non faria quello che ſe partiße da lo istante C da eßo iſtante C che è il ſecondo propoſito. Propoſitione. V. Niun corpo egualmente graue, puo andare per alcun ſpacio di tempo, ouer di loco, di moto naturale, e uiolente inſieme miſto. Esſempi gratia, ſel fuße una poßanza mouente in ponto A la qual doueße tirare un corpo egualmente graue uiolentemente per aere, et che tutto il tranſito: chi far doueße il detto corpo de quella ſpinto: fuße tutta la linea ABCDEF. |
line CD the other. I say that those two bodies, when arriving at the end of their violent movements, that is, the first at the instant or point B and the other at the instant or point D, they travel with the same velocity. But, at the beginning of their movements, that is, the one at the instant A and the other at the instant C, they start with unequal velocities. [This happens] because the one that has to travel along the transit or space AB (as this is longer than the other] starts off faster at the instant A than the other [body] does at the instant C, and this is demonstrated in the following way. If the mentioned two bodies met a resistant at the two instants D and B, where the resistants have a similar and equal resistance, (because of the fifth supposition) they would produce two equal effects. Therefore, (because of the third supposition) they travel with the same velocity [at D and B], which was the first to be shown. In order to demonstrate the second [point of the argument], using our imagination we cut the portion BK from the longer transit or line AB, so that BK is equal to the shorter transit CD. Since the mentioned two bodies, when arriving at the instants D and B, travel with the same velocity (as demonstrated above), then spaces that are equally distant from the mentioned two places or instants D and B have a transit with the same velocity (because of the second supposition). Therefore, the mentioned two bodies travel with the same velocity, the first through the partial space KB and the other through the total space CD, that is, they travel along them in equal times. Since a heavy body travels (with violent motion) more slowly the farther away it is from its beginning, (because of the third supposition), then the body that comes from the instant A travels faster through the space AK than through any other space within the partial space KB. Thus, (according to common knowledge) the body that comes from the instant A travels faster through the space AK than through any other space of the total space CD. The body that comes from the point or instant A therefore starts at this instant A faster than if it had started from the instant C, which was the second [point] to be shown. Fifth proposition. No equally heavy body can travel for an interval of time or a space with a motion mixed of violent and natural motion. For example, let there be a moving power at point A which has to throw an equally heavy body violently through the air, and let it be so that the entire transit accomplished by the mentioned body as pushed by the power is the entire line ABCDEF. |
|
LIBRO PRIMO - 7r - cont. |
FIRST BOOK - 7r - cont. |
|
|
Dico che il detto corpo non paßara parte alcuna di tal ſuo tranſito di moto uiolente, naturale inſieme miſto, ma paßara per quello, ouer totalmente di moto uiolente puro, ouer parte di moto uiolente puro, et parte di moto naturale puro, et quello iſtante, che terminara il moto uiolente, quel medemo ſara principio dil moto naturale, et ſe poßibel fuße (per laduerſario) che quello poteße paſſare alcuna parte di moto uiolente, et naturale inſieme miſto, poniamo, che quella ſia la parte CD. Seguiria adonque che il detto corpo paßando |
I say that the mentioned body does not travel any part of its transit with a motion mixed of violent and natural motions, but travels either only with a pure violent motion, or a part of it with a pure violent motion and another part with a pure natural motion. The instant at which the violent motion stops is the instant at which the natural motion starts. Assuming (as the opponent says) the [body] could travel some part with violent and natural motions mixed together, which may be part CD, it follows therefore that the mentioned body, while going |
|
LIBRO PRIMO - 7v |
FIRST BOOK - 7v |
|
 dal ponto C al ponto D andaße augumentando in uelocita, per quella parte che participaße del moto naturale (per la prima propoſitione) et ſimilmente che andaße calando de uelocita per quella parte che participaße del moto uiolente (per la terza propoſitione) che ſaria una coſa abſorda, che tal corpo in un medemo tempo debbia andar augumentando, et diminuendo de uelocita, destrutto adonque l’oppoſito, rimane il propoſito. Propoſitione. VI. Ogni reſiſtente men uerra offeſo, da un corpo egualmente graue eiecto uiolentemente per aere, in quel iſtante che diſtingue il moto uiolente dal naturale, che in ogni altro luoco. ESſempio ſel fuße una poßanza mouente in ponto A la qual doueße tirare un corpo egualmente graue uiolentemente per aere, et che tutto il tranſito: che tranſir doueſſe quel tal corpo da quella ſpinto, foße tutta la linea ABCDEF, et che il ponto D fuße il luoco de lo iſtante doue ſe ſeparara il moto uiolente dal naturale. Dico che ogni reſiſtente men uerria offeſo dal detto corpo in ponto D che in ogni altro luoco del detto tranſito. Perche il detto corpo andaria piu tardißimo per lo iſtante D che in ogni altro luoco del tranſito uiolente ABCD (per lo primo correlario della terza propoſitione) et conſequentemente faria menor effetto in lui. Similmente perche il detto corpo andaria piu tardißimo per lo iſtante D (per lo primo correlario della prima propoſitione) che in ogni altro luoco del tranſito naturale DEF conſequentemente faria menor effetto in lui, e pero ſel detto reſiſtente fuſſe |
 from point C to point D, increases its velocity according to the ratio by means of which it shares a natural motion (because of the first proposition). Likewise, it decreases its velocity according to the ratio by means of which it shares a violent motion (because of the third proposition). It is absurd that the mentioned body increases and decreases its velocity at the same time. The argument of the opponent is destroyed, therefore only the [previous] argument remains, which was to be shown. Sixth proposition. All resistants are less damaged by an equally heavy body that is violently ejected through the air at the instant that distinguishes the violent from the natural motion than at any other place [on the trajectory]. For example, let there be a moving power at point A that has to throw an equally heavy body violently through the air, and let the entire transit to be traveled by that body, pushed by the power, be the entire line ABCDEF. Let point D be the place of the instant where the violent motion separates from the natural one. I claim that each resistant is less damaged at point D than at any other place of the mentioned transit. Since the mentioned body moves slower at point D than at any other place along the violent transit ABCD, (because of the first corollary of the third proposition), it consequently produces the smallest effect on it. Similarly, since the mentioned body (because of the first corollary of the first proposition) travels slower through the instant D than at any other place of the natural transit DEF, then consequently it produces a smaller effect on it. But, if the mentioned resistant were |
|
LIBRO PRIMO - 8r |
FIRST BOOK - 8r |
|
 percoſſo in ponto C ouer in ponto E dal detto corpo ſaria piu offeſo, che eßendo percoßo in lo detto ponto D perche il detto corpo andaria piu ueloce per lo ponto C (di moto uiolente) et per lo ponto E di moto naturale, che per lo ponto D che è il propoſito. FINE DEL PRIMO LIBRO. |
 hit at point C or at point E by the mentioned body, it would be more damaged than if it were hit at point D because the mentioned body travels faster through point C (with violent motion) and through point E (with natural motion) than through point D, which was to be shown. END OF THE FIRST BOOK. |
|
LIBRO SECONDO - 8v |
SECOND BOOK - 8v |
|
|
Second Book COMINCIA IL SECONDO LIBRO DELLA NOVA SCIENTIA DI NICOLO TARTAGLIA BRISCIANO. DIFFINITIONE PRIMA. MOuimento retto di corpi egualmente graui è quello, che fanno da un loco, a un altro rettamente, cioè per retta linea. Come ſaria a mouerſi dal ponto A al ponto B ſecondo che giace la linea AB.  Diffinitione. II. Mouimento curuo di corpi egualmente graui è quello, che fanno da uno luoco a un’altro curuamente, cioè per curua linea. Come ſaria a mouerſi dal ponto C al ponto D ſi come sta la linea CD. 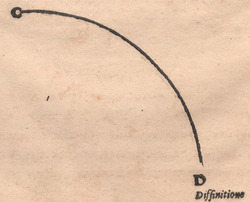
|
THE SECOND BOOK OF THE NEW SCIENCE OF NICOLO TARTAGLIA STARTS. FIRST DEFINITION. The straight movement of equally heavy bodies is accomplished by them moving straightly from one place to the other, that is, along a straight line. This is a movement from point A to point B according to the way line AB lies.  Second definition. A curved movement of equally heavy bodies is accomplished by them moving curvilinearly from one place to the other, that is, along a curved line. This is the movement from point C to point D, according to the line CD. 
|
|
LIBRO SECONDO - 9r |
SECOND BOOK - 9r |
|
|
Diffinitione. III. Mouimento in parte retto e in parte curuo di corpi egualmente graui, è quello, che fanno da uno luoco, a un altro parte rettamente, et parte curuamente, cioe per linea in parte retta, e in parte curua. COme ſaria a dire mouendoſi dal ponto E al ponto G ſi come giace la linea EFG intendando pero che le dette due parte cioe la parte retta EF ſia congionta in diretto con la parte curua FG cioe che non faciano angolo in ponto F perche ſe cauſaſſeno angolo non ſe potria dire che fuſſe un moto continuo anci ſariano dui vari moti, ſi come che anchora non ſe potria dire che tutta la quantita EFG fuſſe vna ſol linea, ma due linee, cioe vna retta, e laltra curua, et queſto biſognaua delucidare.  Diffinitione. III [I]. Orizonte è detto quel piano circulare, che diuide (non ſolamente) lo hemiſperio inferiore dal ſuperiore, ma anchora ogni corpo egualmente graue, quando che è per eſſer eiecto, ouer tirato uiolentemente per aere, in due parti eguali, et è concentrico con il detto corpo. |
Third definition. A movement partially straight and partially curved of equally heavy bodies is accomplished by them moving from one place to the other partially straightly and partially curvilinearly, that is, along a line partially straight and partially curved. This is the movement from point E to point G, according to the way line EFG lies. It is noted, however, that the mentioned two parts, that is, the straight part EF joined together directly with the curved part FG, do not compose any angle at point F. If they did compose an angle, the motion could not be said to be continuous and these would be two different motions. In the same way, the entire quantity EFG could not be said to be one single line but two lines, one straight and the other curved, and this is what was to be elucidated.  Fourth definition.52 The horizon is the circular plane that not only divides the upper hemisphere from the lower, but also divides each equally heavy body into two equal parts. When [the body] is to be ejected, that is, violently thrown through the air, the horizon is concentric to the mentioned body. |
|
LIBRO SECONDO - 9v |
SECOND BOOK - 9v |
|
|
Diffinitione. V. Semidiametro del orizonte, uien detta quella linea, che ſi parte dal centro, e ua a terminare nella circonferentia di quello rettamente per quel uerſo, doue chi debbe eſſer tirato un corpo egualmente graue uiolentemente per aere. Diffinitione. VI. Perpendicolar de l’orizonte è detta quella linea, che ſi parte dal polo de l’orizonte (cognominato zenith) et uien perpendicolarmente ſopra il centro di quello, et continouata per fin al centro dil mondo. Diffinitione. VII. Ma quella parte, che è dal centro al polo, uien detta la perpendicolare ſopra a l’orizonte, et l’altra che è dal detto centro per fin al centro53 del mondo è detta la perpendicolare ſotto à l’orizonte. Diffinitione. VIII. Il tranſito, ouer moto uiolente d’un corpo egualmente graue uien detto eſſer per il pian de l’orizonte quando che in el principio ſe iſtente in parte per il ſemidiametro de l’orizonte. Diffinitione. IX. Il tranſito, ouer moto uiolente d’un corpo egualmente graue, uien detto eſſer elleuato ſopra a l’orizonte quando che in el principio ſe iſtende talmente che quello cauſi in parte angolo acuto con el ſemidiametro de l’orizonte, diſopra a |
Fifth definition. The semidiameter of the horizon is the line that starts from the center and ends on its circumference, straight in the direction toward which an equally heavy body has to be thrown violently through the air. Sixth definition. The perpendicular to the horizon is the line that starts from the pole of the horizon (called Zenith) and arrives perpendicularly at its center and then continues to the center of the world. Seventh definition. That part, which comes from the center of the pole, is called perpendicular above the horizon. The other part, which moves from the mentioned center [of the horizon] to the center54 of the world, is called perpendicular below the horizon. Eighth definition. The transit, that is, the violent motion of an equally heavy body, is defined to be the motion along the plane of the horizon when, during the first part [of its trajectory], it partially follows the semidiameter of the horizon. Ninth definition. The transit, that is, the violent motion of an equally heavy body, is said to be elevated above the horizon when, from its beginning, it partially follows a path so as to compose an acute angle with the semidiameter of the horizon, above |
|
LIBRO SECONDO - 10r |
SECOND BOOK - 10r |
|
|
l’orizonte, et tanto piu ſe dice eſſer elleuato, quanto maggior angolo acuto cauſa, ma quando cauſa angolo retto ſe dice retto ſopra al orizzonte. Diffinitione. X. Il tranſito, ouer moto uiolente d’un corpo egualmente graue ſe dice eſſer elleuato 45 gradi ſopra al orizonte quando che in el principio ſe iſtende talmente, che diuide l’angolo retto, cauſato dalla perpendicolar ſopra al orizonte con il ſemidiametro del orizonte, in due parti eguale. Diffinitione. XI. Il tranſito, ouer moto uiolente d’un corpo egualmente graue, ſe dice eſſer obliquo ſotto al orizonte, quando che in el principio ſe iſtende talmente che quel cauſa angolo acuto con il ſemidiametro del orizonte di ſotto a eſſo orizonte, et tanto piu ſe dice eſſer obliquo quanto maggior angolo acuto cauſa, ma quando cauſa angolo retto, ſe dice retto ſotto al orizzonte. Diffinitione. XII. Li tranſiti ouer moti uiolenti de corpi egualmente graui, ſe dicono egualmente elleuati ſopra al orizonte, quando che in el principio di quegli ſe istendono talmente che cauſano eguali angoli acuti con il ſemidiametro del orizonte di ſopra à eſſo orizonte, et ſimilmente egualmente obliqui, quando che in el detto principio cauſano eguali angoli acuti con il detto ſemidiametro di ſotto a eſſo orizonte. |
the latter. And the more it is said to be elevated, the greater the acute angle is. But when a right angle is composed, it is said to be at right angle above the horizon. Tenth definition. The transit, that is, the violent motion of an equally heavy body, is said to be elevated at 45 degrees above the horizon when, from its beginning, it follows [a line] that divides into two equal parts the right angle, which is between the perpendicular above the horizon and the semidiameter of the horizon. Eleventh definition. The transit, that is, the violent motion of an equally heavy body, is said to be oblique below the horizon when, from its beginning, it follows [a line] that composes an acute angle with the semidiameter of the horizon below the horizon. The greater the composed acute angle, the more oblique it is said to be. If it composes a right angle, it is said to be at right angle below the horizon. Twelfth definition. The transits, that is, the violent motions of equally heavy bodies, are said to be equally elevated above the horizon when, from their beginnings, they follow [lines] that compose equal acute angles with the semidiameter of the horizon, above the same horizon. Likewise, [they are said] to be equally oblique when, from the mentioned beginnings, [they follow a line that] composes equal acute angles with the mentioned semidiameter below the horizon. |
|
LIBRO SECONDO - 10v |
SECOND BOOK - 10v |
|
|
Diffinitione. XIII. Il tranſito, ouer moto uiolente dun corpo egualmente graue uien detto eſſer per la perpendicolar del orizonte, quando che il principio, et fin di quello è in la detta perpendicolare, cioe quando che quello ê retto ſopra, ouer ſotto al orizzonte. Diffinitione. XIIII. La diſtantia dun tranſito, ouer moto uiolente dun corpo egualmente graue, ſe piglia per quello interuallo: che è per retta linea dal principio al fine di tal moto uiolente. Suppoſitione. Prima. Tutti li tranſiti ouer mouimenti naturali de corpi egualmente graui ſono fra loro, et anchora alla perpendicolar de lorizonte equidiſtanti. ABenche dui tranſiti, ouer moti naturali de corpi egualmente graui mai poſciano eſſer fra loro, ne anchora alla perpendicolar de l’orizonte perfettamente equidiſtanti. Perche ſe la terra gli andaſſe cedendo loco ſi come fa l’aere ſenza dubbio concorrariano inſieme nel centro del mondo onde (per la vltima diffinitione del primo de Euclide) non ſariano com’ho detto equidiſtanti. Nientedimeno per eſſer error inſenſibile in vn poco ſpacio. li ſupponemo tutti equidiſtanti fra loro et anchora alla perpendicolar de l’orizonte. Suppoſitione. II. Ogni tranſito, ouer moto uiolente de corpi egualmente graui che ſia fuora della perpendicolar de l’orizonte ſempre ſara in parte retto e in parte curuo, et la parte curua ſara parte d’una circonferentia di cerchio. |
Thirteenth definition. The transit, that is, the violent motion of an equally heavy body, is said to be moving along the perpendicular to the horizon when its beginning and its end are on the mentioned perpendicular, that is, when the transit is at a right angle above or below the horizon. Fourteenth definition. The length of a transit, that is, of the violent motion of an equally heavy body, is the interval along a straight line from the beginning to the end of the violent motion. First supposition. All transits, that is, natural movements of equally heavy bodies, are equidistant to each other and to the perpendicular to the horizon.55 However, two transits, that is, two natural motions of equally heavy bodies, can never be perfectly equidistant to each other and to the perpendicular to the horizon. [This is the case] because, if the earth let them pass, as the air does, they would certainly meet at the center of the world. Therefore (because of the last definition of the first [book] of Euclid) they would not be equidistant, as I said. Nevertheless, as the error cannot be recognized in a short space, we assume them [the transits of natural motions] to be equidistant to each other and to the perpendicular to the horizon. Second supposition. Each transit, that is, each violent motion of equally heavy bodies that does not follow the perpendicular to the horizon, is always partially straight and partially curved. The curved part is a portion of the circumference of a circle. |
|
LIBRO SECONDO - 11r |
SECOND BOOK - 11r |
|
|
ABenche niun tranſito, ouer moto uiolente d’un corpo egualmente graue che ſia fuora delle perpendicolare de l’orizonte mai puol hauer alcuna parte che ſia perfettamente retta per cauſa della grauita che ſe ritroua in quel tal corpo, la quale continuamente lo ua ſtimolando, et tirando uerſo il centro del mondo. Niente di meno quella parte che è inſenſibilmente curua, La ſupponemo retta, et quella che è euidentemente curua la ſupponemo parte duna circonferentia di cerchio, perche non preteriſcono in coſa ſenſibile. Suppoſitione. III. Ogni corpo egualmente graue, in fine de ogni moto uiolente, che ſia fuora della perpendicolare di l’orizonte ſi mouera di moto naturale, il qual ſara contingente con la parte curua dil moto uiolente. ESſempi gratia ſe vn corpo egualmente graue ſara eietto ouer tratto violentemente per aere, fuora della perpendicolar de l’orizonte. Dico che in fine di tal moto uiolente, (non trouando reſiſtentia) ſi mouerà di moto naturale, il quale ſara contingente con la parte curua dil moto violente alla ſimilitudine de tutta la linea ABCD de la quale tutta la parte ABC ſara il tranſito dil moto violente, et la parte CD ſara il tranſito fatto di moto naturale, il qual ſara continuo, et contingente con la parte curua BC in ponto C.56 queſto è quello che uolemo inferire.  Suppoſitione. IIII. Lo effetto piu lontano dal ſuo principio, che far poſſa un |
Indeed, the transit, that is, the violent motion of an equally heavy body that does not follow the perpendicular to the horizon, never shows any perfectly straight part because of the gravity in that body which continuously pulls it toward the center of the Earth. Nevertheless, that part [of the transit] that is not perceived as being curved is assumed to be straight, and that part that is evidently curved is assumed to be part of the circumference of a circle, as this [assumption] does not influence the argument. Third supposition. Each equally heavy body that does not follow the perpendicular to the horizon after the end of each violent motion moves by natural motion, which is joined together with the curved part of the violent motion. For example, let there be an equally heavy body ejected or thrown violently through the air so that it does not follow the perpendicular to the horizon. I say that at the end of such violent motion (if it does not meet resistance), it moves with natural motion, which is joined together with the curved part of the violent motion as is shown by the entire line ABCD. Of this line, part ABC is the transit of the violent motion and part CD the transit accomplished with natural motion. This is joined together and continuous to the curved part BC at point C.57 This is what we want to infer.  Fourth supposition. The farthest effect, produced by |
|
LIBRO SECONDO - 11v |
SECOND BOOK - 11v |
|
|
corpo egualmente graue di moto uiolente ſopra a qualunque piano, ouer ſopra a qualunque retta linea, e quello che termina preciſamente in eſſo piano, ouer in eſſa linea (eſſendo eiecto ouer tirato da una medema poſſanza mouente.) ESſempi gratia ſia una poſſanza mouente in ponto A la qual habbia eiecto, ouer tirato il corpo B egualmente graue uiolentemente per aere, il cui tranſito ſia la linea AEDB et il ponto D poniamo ſia lo iſtante, che diſtingue il tranſito, ouer moto uiolente AED dal tranſito, ouer moto naturale DB et dal ponto A al ponto D ſia protratta la linea ADC hor dico che il ponto D e il piu lontan effetto dal ponto A che far poſſa il detto corpo B ſopra la linea  ADC ouer ſopra quel piano doue è ſita la detta linea ADC coſi conditionatamente eleuato. Perche ſe la detta poßanza A traeſſe il medemo corpo B piu elleuatamente ſopra à l’orizonte, quel faria il ſuo effetto di moto naturale ſopra la medema linea ADC come appar in la linea, ouer tranſito AFG in ponto G il qual effetto G dico che ſaria piu propinquo al ponto A cioe al principio di tal moto di quello, che ſara lo effetto D perche il detto corpo B non |
an equally heavy body [that moves] with violent motion on whichever plane or whichever straight line, is the one that happens precisely on that plane or on that line (if it is ejected or thrown by the same moving power). Let there be a moving power at point A which has ejected or thrown the equally heavy body B through the air. Its transit would be the line AEDB, where point D is assumed to be the instant that distinguishes the transit or violent motion AED from the transit or natural motion DB. Let line ADC be prolonged from point A to point D. I say that at point D the farthest effect from point A is produced by the mentioned body B above line  ADC, that is, above that plane where line ADC is placed and elevated like the same line. If the mentioned power A threw the same body B to a more elevated position above the horizon, it would produce its effect along the natural motion on the same line ADC, as the line or transit AFG shows, at point G. I say that the effect G is closer to point A, that is, to the beginning of that motion, than the effect D. This is because the mentioned point B does not |
|
LIBRO SECONDO - 12r |
SECOND BOOK - 12r |
|
|
ueneria a terminare in la detta linea ADC di moto uiolente, anci terminaria di ſopra di quella in ponto F et quanto piu fuſſe elleuatamente tirato, tanto piu ſe andaria accoſtando co’l ſuo effetto al detto ponto A ſopra la detta linea ADC perche ancora il moto uiolente di quello, tanto piu ſe andaria ſcoſtando col ſuo termine dalla detta linea ADC cioè piu in alto terminando. Similmente ſe la medema poſſanza traeſſe il medemo corpo B men elleuato dil tranſito, ouer linea AED alla ſimilitudine del tranſito, ouer linea AIHK quel faria il ſuo effetto di moto uiolente ſopra la detta linea ADC alla ſimilitudine dil ponto H il qual effetto H dico che ſaria piu propinquo al ponto A de quel fatto in ponto D perche il ſin di tal moto uiolente andaria a terminare di ſotto della detta linea ADC in ponto K et quanto piu la detta poſſanza A ſe andaſſe arbaßando in tirare il detto corpo B tanto piu il detto corpo B andaria facendo il ſuo effetto piu propinquo al ponto A ſopra la detta linea ADC perche quanto piu la ſe andaſſe arbaſſando, tanto piu il ſuo moto uiolente andaria a terminare di ſotto della detta linea ADC il medemo ſi deue intendere in ogni altro tiro eſſempi gratia tirando dal ponto A al ponto F (termine dil moto uiolente AF) la linea AFL dico che il detto corpo B in altro modo tirato dalla medema poſſanza mai potria aggiongere al detto ponto F come ſi manifeſta nel tranſito AEDB il qual ſega la detta linea AFL in ponto M il qual ponto M e molto piu propinquo al ponto A di quello che è il detto ponto F. Similmente ancora tirando una linea dal detto ponto A al ponto K (termine dil moto violente AIK ) quala ſia AKN dico che il detto corpo B in altro diuerſo modo tirato dalla medema poſſanza mai potria aggiongere al detto ponto K come per eſſempio appar nelli altri dui tiri ſuperiori che ciaſcaduno ſegan la detta linea AKN di moto naturale nelli dui ponti O et P che cadauno di loro è piu propinquo al ponto A di quello chi è il detto ponto K è queſto è quello che uolemo inferire. Propoſitione. Prima. Li quatro angoli d’ogni quadrilatero rettilineo ſono eguali a quatro angoli retti. SIa il quadrilatero ABCD dico tutti li ſuoi quatro angoli tolti inſieme ſono eguali a quatro angoli retti. Perche protratto lo diametro DB ſara diuiſo in dui triangoli, et li trei angoli di cadauno de detti triangoli (per la ſeconda parte della 32 del I di Euclide) ſono eguali a dui angoli retti, onde tutti li 6 angoli de detti dui triangoli ſono eguali a quatro angoli retti, et perche li detti 6 angoli di detti 2 triangoli ſono eguali alli 4 angoli del detto quadrilatero, |
end its violent motion on the mentioned line ADC. But it ends that motion higher than that line at point F. The more elevated [the angle at which] the body is thrown, the closer its effect is to the mentioned point A on the mentioned line ADC, because the end of its violent motion is farther away from the mentioned line ADC, that is, the motion ends at a higher point. Similarly, if the same power threw the same body B along a less elevated transit or line than AED, like the transit or line AIHK, it would produce its effect by violent motion above the mentioned line ADC at point H. I say that such effect [at point] H is closer to point A than the effect at point D because the end of such violent motion ends below the mentioned line ADC at point K. [This happens] because the lower the mentioned power A is, the deeper its violent motion ends below the mentioned line ADC. The same is valid for any other shot. For example, let line AFL be produced from point A to point F (which is the end of the violent motion AF). I say that the mentioned body B, thrown in whichever way by the same power, will never be able to reach the mentioned point F. This is manifested by the transit AEDB that cuts the mentioned line AFL at point M, and this point M is much closer to point A than the mentioned point F. Similarly, a line from the mentioned point A to point K is produced (which is the end of the violent motion AIK) so as to achieve line AKN. I say that the mentioned body B will never be able to reach the mentioned point K, no matter how it is thrown by the same power. This is clear, for example, in reference to the other two upper shots which cut the mentioned line AKN of natural motion at the two points O and P. Each of these points are closer to point A than to the mentioned point K. This was what we wanted to infer. First proposition. The four angles of each rectilinear quadrilateral are equal to four right angles. Let there be the quadrilateral ABCD. I say that all of its four angles considered together are equal to four right angles. Given the diameter DB, [the quadrilateral] is divided into two triangles. The three angles of each of the mentioned triangles (because of the second part of the thirty-second [proposition] of the first [book] of Euclid) are equal to two right angles. Therefore all six angles of the mentioned two triangles are equal to four right angles. Then, the mentioned six angles of the mentioned two triangles are equal to the four angles of the mentioned quadrilateral. |
|
LIBRO SECONDO - 12r - cont. |
SECOND BOOK - 12r - cont. |
|
|
eſſempi gratia langolo ABD del triangolo ABD gionto con langolo DBC del triangolo DBC ſe egualiano a tutto langolo ABC del quadrilatero, et ſimilmente li altri dui, che terminano al ponto D ſe egualiano a tutto langolo ADC del detto quadrilatero, et li altri dui, cioè langolo A et C ſono quelli isteßi del quadrilatero, onde il propoſito è manifeſto. |
Let there be, for example, the angle ADB of triangle ADB joined together with angle DBC of triangle DBC. They are equal to the entire angle ABC of the quadrilateral. Likewise, the other two, which are placed at point D, are equal to the entire angle ADC of the mentioned quadrilateral. The other two angles, that is, the angles at point A and at point C, are the same as the angles of the quadrilateral. Therefore it is manifested what was to be shown. |
|
LIBRO SECONDO -12v |
SECOND BOOK - 12v |
|
 Propoſitione. II. Se dal centro dun cerchio ſaran protratte due linee fina alla circonferentia, tal proportione hauer a tutta la circonferentia del cerchio à l’arco che interchiuden le dette due linee qual hauera quatro angoli retti a langolo contenuto dalle dette due linee ſopra il centro. SIa il cerchio ABC il centro dil quale ſia il ponto D et dal centro D ſian protratte le due linee DA et DB. Dico che tal proportione ha tutta la circonferentia del detto cerchio a larcho AB che interchiude le dette due linee qual ha quattro angoli retti, à langolo ADB. Perche protraro vna delle dette linee fina alla circonferentia et ſia AD fina in E onde (per la vltima dil ſeſto de Euclide) la proportione de l’arco EB a l’arco BA è ſi come l’angolo EDB a l’angolo BDA et (per la 18 del quinto de Euclide) il congionto delli detti dui archi EB et BA (cioe tutto l’arco EBA) a l’arco BA ſara ſi come il congionto delli dui angoli EDB et BDA a l’angolo BDA et perche l’arco EBA è la mitade della circonferentia di tutto il cerchio, et il congiunto delli dui angoli EDB et BDA (per la decimatertia del primo de Euclide) è eguale a dui angoli retti ſeguita adonque che ſi come è la mita della circonſerentia del detto cerchio al detto arco BA coſi ſara dui angoli retti a l’angolo BDA et perche tutta la circonferentia dil cerchio alla mitade di quella (cioe a l’arco EBA) è ſi come quatro angoli retti, a due angoli retti, donque (per la uiceſimaſeconda del quinto de Euclide) ſi come tutta la circonferentia del detto cerchio a l’arco AB coſi ſaran quatro angoli retti a l’angolo BDA che è il propoſito. |
 Second proposition. If two lines are produced from the center of a circle to the circumference, the ratio between the entire circumference of the circle and the arc delimited by the mentioned two lines is the same as it is between four right angles and the angle contained by the mentioned two lines at the center. Let there be the circle ABC whose center is point D. From center D two lines are produced, that is, DA and DB. I say that the entire circumference of the mentioned circle has the same ratio to the arc AB, delimited by the mentioned two lines, as four right angles have to the angle ADB. I prolong one of the mentioned lines to the circumference and AD to E. Therefore, (due to the last [proposition] of the sixth [book] of Euclid) the ratio of arc EB to arc BA is the same as the ratio of angle EDB to angle BDA and (because of the eighteenth [proposition] of the fifth [book] of Euclid) the ratio of the sum of the mentioned two arcs EB and BA (that is, the entire arc EBA) to arc BA is the same as the ratio of the sum of the two angles EDB and BDA to angle BDA, and since the arc EBA is half of the circumference of the entire circle, and since the sum of the two angles EDB and BDA (because of the tenth [proposition] of the first [book] of Euclid) is equal to two right angles, it follows that the ratio between half of the circumference of the mentioned circle to the mentioned arc BA is the same as that of two right angles to the angle BDA. Since the ratio of the entire circumference to its half (that is, arc EBA) is like the ratio of four right angles to two right angles, (because of the twenty-second [proposition] of the fifth [book] of Euclid) the ratio of the circumference of the mentioned circle to arc AB is the same as the ratio of four right angles to angle BDA, which was to be shown. |
|
LIBRO SECONDO - 13r |
SECOND BOOK - 13r |
|
 Propoſitione. III. Se due linee rette congiunte angolarmente contingerano un cerchio, et produtta una di quelle dalla banda doue l’angolo, tal proportione hauera la circonferentia dil cerchio à l’arco che interchiuderanno, qual haueranno quattro angoli retti à l’angolo exterior cauſato dalla linea protratta. SIano le due linee AB et BC congionte angolarmente in ponto B le quale contingano il cerchio DEFG in li dui ponti D et F et ſia protratta una di quelle dalla banda uerſo B et ſia la FB protratta fina in ponto H. Dico che tal proportione hauera la circonferentia dil cerchio a l’arco DEF qual ha quatro angoli retti à l’angolo DBH. Perche del centro del detto cerchio (qual pongo ſia K) tiro le due linee KD et KF onde (per la prima propoſitione di queſto) li quatro angoli del quadrilatero BDKF ſono eguali a quatro angoli retti, et perche cadauno delli dui angoli KDB et KFB (per lo correlario della decimaquinta del tertio de Euclide) è retto. Seguita adonque |
 Third proposition. If two straight lines are angularly joined together and tangent to a circle and if one of the two lines is prolonged at the side where the angle is, the circumference of the circle has the same ratio to the arc delimited by the lines as the four right angles to the external angle built on the prolonged line. Let the two lines AB and BC be angularly joined together at point B and let them be tangent to the circle DEFG at points D and F. Let one of the two lines on the side of B be prolonged and FB prolonged until H. I say that the circumference of the circle has the same ratio to the arc DEF as four right angles have to the angle DBH. From the center of the mentioned circle (which I call K), I produce the two lines KD and KF. Hence (because of the first proposition of this [book]), the four angles of the quadrilateral BDKF are equal to four right angles. Since each of the two angles KDB and KFB (because of the corollary of the fifteenth [proposition] of the third [book] of Euclid) is right, it follows |
|
LIBRO SECONDO - 13v |
SECOND BOOK - 13v |
|
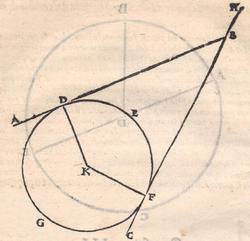 che li altri dui inſieme (cioè l’angolo DBF et l’angolo FKD) ſiano ancora loro eguali a dui angoli retti, et [(]per la decimatertia del primo de Euclide) li dui angoli DBF et DBH ſono ſimelmente eguali a dui angoli retti, onde (per la prima conceptione del primo de Euclide) li dui angoli DBF et DBH sono eguali alli dui angoli DBF et DKF leuando adunque communamente da l’una e l’altra parte lo angolo DBF reſtara (per la terza conceptione del primo de Euclide) l’angolo DBH eguale a l’angolo DKF onde (per la ſettima propoſitione del quinto de Euclide) quatro angoli retti a cadauno de loro haueranno una medema proportione, et tal proportione qual ha quatro angoli retti a l’angolo DKF tal hauera la circonferentia del cerchio a l’arco DEF. Adonque (per la II del 5 de Euclide) tal proportione hauera la circonferentia del cerchio a l’arco DEF qual hauera quatro angoli retti a l’angolo exteriore DBH che è il propoſito. Propoſitione. IIII. Se il tranſito ouer moto uiolente dun corpo egualmente graue ſara per il piano de lorizonte, la parte curua di quello |
 that the other two [angles] together (that is, angle DBF and angle FKD) are also equal to two right angles. [(]Due to the thirteenth [proposition] of the first [book] of Euclid), the two angles DBF and DBH are similarly equal to two right angles. Therefore, (because of the first common sentence [axiom] of the first [Book] of Euclid) the two angles DBF and DBH are equal to the two angles DBF and DKF. Consequently, if angle DBF is taken away from both the one and the other side (due to the third common sentence [axiom] of the first of [book] of Euclid), angle DBH becomes equal to angle DKF. Hence (because of the seventh proposition of the fifth [book] of Euclid), four right angles have the same ratio to each of these [two angles] and the ratio of the four right angles to angle DKF is the same as that of the circumference of the circle to arc DEF. Therefore (because of the eleventh [proposition] of the fifth [book] of Euclid), the circumference of the circle has the same ratio to arc DEF as four right angles do to the external angle DBH, which was to be shown. Fourth proposition. If the transit, that is, the violent motion of an equally heavy body moves along the plane of the horizon, its curved part |
|
LIBRO SECONDO - 14r |
SECOND BOOK - 14r |
|
|
ſara la quarta parte della circonferentia del cerchio donde deriua. SIa el ſemidiametro del pian de l’orizonte la linea AB et la perpendicolar del orizonte la linea CAD et il tranſito uiolente d’un corpo egualmemente graue la linea AEF la parte curua dil quale ſia l’arco EF et la parte FG ſia il tranſito fatto di moto naturale. Dico che la detta parte curua EF eſſer la quarta parte della circonferentia del cerchio donde deriua. Perche produro il tranſito naturale GF uerſo il ſemidiametro del orizonte talmente che concorra con quello in ponto H et perche il tranſito FGH é equidiſtante (per la prima suppoſitione di queſto) alla perpendicolar CAD l’angolo adonque FHA (per la prima parte della uigeſimanona del primo de Euclide) ſara eguale a l’angolo HAC il quale é retto, adonque l’angolo FHB exteriore (per la decimaterza del primo de Euclide) ſara retto, onde quatro angoli retti uengono a eſſer quadrupli al detto angolo exteriore per il che la circonferentia del cerchio donde deriua la detta parte curua EF (per la terza propoſitione di questo) uien a eſſer quadrupla al detto arco EF adonque il detto arco EF uien a eſſer il quarto della circonferentia dil cerchio donde deriua, che é il propoſito. 
|
is the fourth part of the circumference of the circle from which [that part] derives. Let line AB be the semidiameter of the plane of the horizon and line CAD the perpendicular to the horizon. The line EAF is the violent transit of an equally heavy body and its curved part is the arc EF. Let the part FG be the transit accomplished by natural motion. I say that the mentioned curved part EF is the fourth part of the circumference of the circle from which [the curved part] derives. I prolong the natural transit GF toward the semidiameter of the horizon so that they meet at point H. Since the transit FGH (because of the first supposition of this [book]) is equidistant to the perpendicular CAD, (because of the first part of the twenty-ninth [proposition] of the first [book] of Euclid) angle FHA is equal to angle HAC, which is a right angle. Therefore, the external angle FHB (because of the thirteenth [proposition] of the first [book] of Euclid) is right and thus four right angles are quadruple the mentioned external angle. From this [it follows] that the circumference of the circle from which the mentioned arc EF derives (because of the third proposition of this [book]) is quadruple the mentioned arc EF. Therefore, the mentioned arc EF is a fourth of the circumference of the circle from which it derives, which was to be shown. 
|
|
LIBRO SECONDO - 14v |
SECOND BOOK - 14v |
|
|
Propoſitione. V. Se il tranſito, ouer moto uiolente d’un corpo egualmente graue ſara elleuato ſopra a l’orizonte, la parte curua di quello ſara maggiore della quarta parte della circonferentia del cerchio donde deriua, et quanto piu ſara eleuato, tanto piu ſara maggiore di la quarta parte de detta circonferentia, et tamen mai potra eſſer la mitade di eſſa circonferentia. SIa il ſemidiametro del pian dell’orizonte la linea AB et la perpendicolar de l’orizonte la linea CAD et il tranſito uiolente d’un corpo egualmente graue la linea AEF la parte curua dil quale ſia l’arco EF et la parte FG ſia il tranſito fatto di moto naturale. Dico l’arco EF eſſer maggiore della quarta parte della circonferentia del cerchio donde deriua. Perche produro il tranſito naturale FG et la parte retta AE tanto che concorrano inſieme in ponto H et produro FH fin in K coſtituendo l’angolo eſteriore 
|
Fifth proposition. If the transit, that is, the violent motion of an equally heavy body, is elevated above the horizon, its curved part is bigger than the fourth part of the circumference from which it [the curved part] derives. And the more [the transit] is elevated, the bigger than the fourth part of the mentioned circumference [the curved part] is, and it can never be the half of that circumference. Let line AB be the semidiameter of the plane of the horizon and line CAD the perpendicular to the horizon. Let line EAF be the violent transit of an equally heavy body and its curved part line EF. Let part FG be the transit accomplished by natural motion. I say that the arc EF is bigger than the fourth part of the circumference of the circle from which [that curved part] derives. I prolong both the natural transit FG and the straight part AE so that they meet at point H. Then I prolong FH until point K in order to compose the external angle 
|
|
LIBRO SECONDO - 15r |
SECOND BOOK - 15r |
|
|
EHK et perche l’angolo FHE è eguale (per la prima parte della uigeſima nona del primo de Euclide) a l’angolo EAC et l’angolo EAC (per la ultima conceptione del primo de Euclide) è menore d’un angolo retto, adonque l’angolo EHF (per comuna ſententia) ſarà minore d’un angolo retto, onde l’angolo EHK eſteriore (per la 13 del primo de Euclide) ſara maggiore d’un angolo retto, et (per la ſeconda parte della ottaua del quinto de Euclide) quatro angoli retti haueranno menore proportione che quadrupla al detto angolo eſteriore, et ſimelmente la circonferentia del cerchio donde deriua l’arco EF (per la terza propoſitione di queſto) hauera menor proportion che quadrupla, al detto arco, et (per la ſeconda parte della decima del 5. de Euclide) l’arco EF ſara maggiore della 4 parte della circonferentia dil cerchio donde deriua che é il primo propoſito. Et perche quanto piu ſe andara eleuando ſopra a l’orizonte la parte retta AE tanto piu menor angolo andara cauſando la linea AE con la linea AC et conſequentemente la linea EH con la linea FH et l’angolo EHK continuamente ſe andara agrandando et la proportione de quatro angoli retti a quello ſminuendo di quadrupla et ſimelmente la proportion della circonferentia del cerchio donde deriua l’arco EF al detto arco EF ſe andara ſminuendo di quadrupla per il che il detto arco EF (per la detta ſeconda parte della decima del quinto di Euclide) andara continuamente creſcendo in parte maggiore d’un quarto de circonferentia che è il ſecondo propoſito. Et perche l’angolo EHK eſteriore mai ſe puo egualiare (per la prima parte della trigeſimaſeconda del primo de Euclide aiutando con la 17 del medemo) a dui angoli retti, adonque la proportion de quatro angoli retti al detto angolo eſteriore mai puo eſſer dupla ſeguita adonque che la proportion della circonferentia del cerchio d’onde deriva qualunque arco, ouer parte curua d’un moto uiolente, mai puo eſſer dupla al detto arco, ouer parte curua, et conſequentemente il detto arco, ouer parte curua mai potra eſſer la mitade della circonferentia del cerchio donde deriua, che è il terzo propoſito. Propoſitione. VI. Se il tranſito, ouer moto uiolente d’un corpo egualmente graue ſara obliquo ſotto a l’orizonte la parte curua di quello ſara menor della quarta parte della circonferentia del cerchio d’onde deriua, et tanto piu ſara menore quanto piu ſara obliquo. |
EHK. Since angle FHE (because of the first part of the twenty-ninth [proposition] of the first [book] of Euclid) is equal to angle EAC and [this] angle EAC (due to the last common sentence [axiom] of the first [book] of Euclid) is smaller than a right angle, angle EHF (for common knowledge) is smaller than a right angle. Thus, the external angle EHK (because of the thirteenth [proposition] of the first [book] of Euclid) is greater than a right angle. Then (because of the second part of the eighth [proposition] of the fifth [book] of Euclid), four right angles have less than a quadruple ratio to the mentioned external angle and, likewise, the circumference of the circle from which the arc EF derives (because of the third proposition of this [book]) has less than a quadruple ratio to the mentioned arc. Therefore (because of the second part of the tenth [proposition] of the fifth [book] of Euclid), arc EF is bigger than the fourth part of the circumference of the circle from which it derives, which was to be shown firstly. Since the more the straight part AE is elevated above the horizon, the smaller the angle composed by line AE with line AC, consequently line EH together with line FH and the angle EHK continuously increase and the ratio of four right angles to that [angle] will also continuously decrease from the quadruple. Similarly, the ratio of the circumference of the circle from which arc EF derives to the same mentioned arc EF also decreases from the quadruple and, therefore, the mentioned arc EF (because of the mentioned second part of the tenth [proposition] of the fifth [book] of Euclid) becomes increasingly longer than one fourth of the circumference, which was to be shown secondly. Since the external angle EHK (because of the first part of the thirty-second [proposition] of the first [book] of Euclid and with the help of the seventeenth of the same [book]) can never be equal to two right angles, the ratio of four right angles to the mentioned external angle can never be the double. Therefore, it follows that the ratio of the circumference of the circle from which any arc may derive, that is, whichever curved part of violent motion, can never be double the mentioned arc or curved part. Consequently, the mentioned arc or curved part, can never be half of the circumference of the circle from which [the curved part] derives, which was to be shown thirdly. Sixth proposition. If the transit, that is, the violent motion of an equally heavy body, is oblique below the horizon, its curved part is smaller than the fourth part of the circumference of the circle from which [that curved part] derives, and the smaller, the more oblique [the transit] is. |
|
LIBRO SECONDO - 15r - cont. |
SECOND BOOK - 15r - cont. |
|
|
SIa il ſemidiametro de l’orizonte la linea AB et la perpendicolare de l’orizonte la linea CAD, et il tranſito uiolente d’un corpo egualmente graue la linea AEF la parte curua, dil quale ſia l’arco EF et la parte FG ſia il tranſito fatto di moto naturale. Dico lo detto arco EF eſſer menore della quarta parte della circonferentia dil cerchio donde deriua. Perche produro il tranſito naturale |
Let line AB be the semidiameter of the horizon, line CAD the perpendicular of the horizon and line AEF the violent transit of an equally heavy body. Let arc EF be its curved part and part FG the transit accomplished by natural motion. I say that the mentioned arc EF is smaller than the fourth part of the circumference of the circle from which it derives. I prolong the natural transit |
|
LIBRO SECONDO - 15v |
SECOND BOOK - 15v |
|
 FG et la parte retta AC tanto che concorrano inſieme in ponto B et produro FH58 fin in K conſtituendo l’angolo esteriore EHK et perche l’angolo FHE é eguale (per la I parte della 29 del I de Euclide) a l’angolo EAC et l’angolo EAC (per la ultima conceptione del primo de Euclide) è maggiore d’un angolo retto (cioe de l’angolo BAC ſua parte) adonque l’angolo EHF ſara maggiore d’un angolo retto onde l’angolo EHK eſteriore (per la decimaterza del primo de Euclide) ſara minore d’un angolo retto, et (per la ſeconda parte della ottaua del quinto di Euclide) quatro angoli retti haueranno a quello maggiore proportione che quadrupla, et ſimilmente la circonferentia del cerchio donde deriua l’arco EF al detto arco EF hauera maggior proportione che quadrupla (per la terza propoſitione di questo) et (per la ſeconda parte della decima del quinto de Euclide) l’arco EF ſara minore della quarta parte della circonferentia del cerchio donde deriua che è il I propoſito. Et perche quanto piu ſe andara arbaßando ſotto a l’orizonte tanto piu la linea EA maggior angolo andara cauſando con la linea CA et conſequentemente la linea FH con la linea EH et continuamente l’angolo EHK eſteriore ſe andara ſminuendo, et la proportione de 4 angoli retti a quello augumentando piu di quadrupla, et ſimilmente la proportione della circonferentia del cerchio d’onde deriua l’arco EF al detto arco EF ſi andara augumentando piu di quadrupla, per il che il detto arco EF (per la detta ſeconda parte della decima del quinto de Euclide) andara continuamente |
 FG and the straight part AE so that they meet at point B. I then prolong line FH59 up to point K so that the external angle EHK is composed. Since angle FHE is equal (because of the first part of the twenty-ninth [proposition] of the first [book] of Euclid]) to angle EAC and since angle EAC (because of the last common sentence [axiom] of the first [book] of Euclid) is greater than a right angle (that is, than the angle BAC which is a part of it), the angle EHF is greater than a right angle and therefore the external angle EHK (because of the thirteenth [proposition] of the first [book] of Euclid) is smaller than a right angle. (Because of the second part of the eighth [proposition] of the fifth [book] of Euclid) four right angles have a ratio greater than quadruple [the external angle EHK]. Similarly, the circumference from which the arc EF derives has a ratio greater than quadruple that same arc EF (because of the third proposition of this [book]). Then (because of the second part of the tenth [proposition] of the fifth [book] of Euclid), the arc EF is smaller than the fourth part of the circumference of the circle from which it derives, which was to be shown firstly. Then, the lower it is below the horizon, the bigger the angle composed by line EA with line CA and consequently, line FH with line EH. The external angle EHK continuously decreases and the ratio of the four right angles to that [external angle EHK] increases more than fourfold. Similarly, the ratio of the circumference of the circle from which the arc EF derives to the same arc EF increases more than fourfold. For these reasons, the mentioned arc EF (because of the mentioned second part of the tenth [proposition] of the fifth [book] of Euclid) becomes continuously |
|
LIBRO SECONDO - 16r |
SECOND BOOK - 16r |
|
|
ſminuendo in parte minore d’un quarto della circonferentia del cerchio d’onde deriuara, che per il ſecondo propoſito. Propoſitione. VII. TVtti li tranſiti, ouer moti uiolenti de corpi egualmente graui, ſi grandi come picoli egualmente eleuati ſopra a l’orizonte, ouer egualmente obliqui, ouer ſiano per il pian de l’orizonte ſono fra lor ſimili, et conſequentemente proportionali, et ſimilmente le diſtantie loro. SIa il ſemidiametro del pian de l’orizonte la linea AB et la perpendicolare de l’orizonte la linea CAD et li tranſiti di dui diuerſi corpi egualmente graui egualmente eleuati ſopra a l’orizonte, le due linee AEFG60 et AHIK di quali le due parti AEF et AHI ſian li tranſiti fatti di moto uiolente, et le due parti FG et IK ſian li tranſiti fatti de moto naturale, et le due parti AE et AH ſiano le lor parti rette, le qual parti rette (per eſſer quegli egualmente eleuati) formarono inſieme una ſol rettitudine, cioe una ſol linea, la qual ſara la linea AEH et dal ponto A ſia dutta la linea AF et quella protratta et continuata direttamente de neceßita andara per il ponto I perche quando le parti rette de tranſiti, ouer moti uiolenti ſi compongano inſieme ancora le loro diſtantie ſe componeranno inſieme (aliter ſeguiria inconueniente aſſai) hor. Dico che il tranſito AEF (fatto di moto uiolente) è ſimile al tranſito AEHI (pur fatto di moto uiolente) et conſequentemente proportionale, et ſimelmente la diſtantia AF alla diſtantia AI. Perche produro li lor tranſiti naturali, et la lor comuna parte retta AEH fin a tanto che concorrano inſieme in li dui ponti L, M et produro li detti tranſiti naturali fin in N, O (coſtituendo li dui angoli eſteriori ELN et LMO) et ducero le due corde EF et HI alle lor parte curue Et perche li dui tranſiti naturali GN et KO (per la prima suppoſitione di queſto) ſono equidiſtanti, adonque l’angolo ELN (per la ſeconda parte della 29 del I de Euclide[)] ſara eguale a l[’]angolo LMO onde (per la ſeconda parte della 7 del 5 de Euclide) quatro angoli retti haueran vna medema proportione à cadaun di loro, et ſimelmente la circonferentia de cadauno di dui cerchij donde deriuano li dui archi EF et HI alli detti dui archi (cadauno al ſuo relatiuo[)] (per la terza propoſitione di queſto) haueranno una medema proportione per la qual coſa l’arco EF uien a eſſer ſimile a l’arco HI et ſimilmente la portion P alla portion Q |
smaller than the fourth part of the circumference of the circle from which it derives, which was to be shown secondly. Seventh proposition. All transits, that is, violent motions of equally heavy bodies, big and small, equally elevated above the horizon, or equally oblique, or moving along the plane of the horizon, are similar and consequently proportional to each other. Their distances are similar and proportional to each other. Let line AB be the semidiameter of the plane of the horizon and line CAD the perpendicular to the horizon. Let lines AEFG61 and AHIK be the transits of two equally heavy bodies also equally elevated above the horizon. Let the two parts of AEF and AHI be the transits accomplished by violent motion and the parts FG and IK the transits also accomplished by natural motion. Let their parts AE and AH be straight. These straight parts (as they are equally elevated) together compose one straightness, that is, only one line and this line is AEH. Let line AF then be produced from point A and then let it be prolonged on the same line so that it inevitably meets point I because if the straight parts of the transits, that is, of the violent motions, are composed together [on the same line], then also their lengths are added together [on the same line] (otherwise a very relevant problem would follow). Now I say that transit AEF (accomplished by violent motion) is similar to transit AEHI (also accomplished by violent motion). Consequently, they have the same ratio to each other as distance AF has to distance AI. I prolong their natural transits and their common straight part AEH so that they meet at the two points L and M and then I prolong their natural transits to the points N and O (composing the two external angles ELN and LMO). Then I produce the two chords EF and HI to their curved parts. Since the two natural transits (because of the first supposition of this [book]) are equidistant, the angle ELN (because of the second part of the twenty-ninth [proposition] of the first [book] of Euclid[)] is equal to angle LMO. Therefore (because of the second part of the seventh [proposition] of the fifth [book] of Euclid), four right angles have the same ratio to each of the [angles ELN and LMO]. Similarly, the circumference of each of the two circles from which the arcs EF and HI derive (correspondingly[)] have the same ratio to the mentioned two arcs (because of the third proposition of this [book]). For this reason, arc EF is similar to arc HI and, in the same way, portion P to portion Q. |
|
LIBRO SECONDO - 16r - cont. |
SECOND BOOK - 16r - cont. |
|
|
onde costituendo ſopra cadauno de detti archi un angolo quai ſiano EPF et HQI li quai dui angoli (per il conuerſo delle due ultime diſſinitione del terzo de Euclide) ſaranno fra loro eguali per la qual coſa l’angolo FEA (per la 31 del terzo de Euclide) ſara eguale a l’angolo IHE onde (per la uigeſimaottaua del I de Euclide) la corda EF ſara equidiſtante alla corda IH per la qual coſa l’angolo EFA ſara eguale (per la ſeconda parte della uigeſimanona del primo de Euclide) a l’angolo FIH adonque il triangolo AEF ſara equiangolo al triangolo AHI et conſequentemente ſimile, onde tal proportione é della |
Let there then be an angle composed above each of the mentioned arcs. These are EPF and HQI. These two angles (because of the converse of the two last definitions of the third [book] of Euclid) are equal to each other. For this reason, angle FEA (because of the thirty-first [proposition] of the third [book] of Euclid) is equal to angle IHE. Therefore (because of the twenty-eighth [proposition] of the first [book] of Euclid), chord EF is equidistant to chord IH. For this reason, angle EFA (because of the the second part of the twenty-ninth [proposition] of the first [book] of Euclid) is equal to angle FIH. Consequently, the triangle AEF has the same angles as the triangle AHI and thus they are similar to each other. Therefore, |
|
LIBRO SECONDO - 16v |
SECOND BOOK - 16v |
|
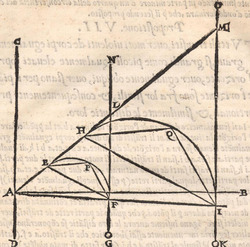 parte retta AE alla parte retta AH qual è dalla corda EF alla corda HI et della diſtantia AF alla diſtantia AI et da l’arco EF à l’arco HI che è il propoſito, et per li medemi modi è uie ſe dimostrara tal ſimilitudine in li tranſiti, ouer moti uiolenti che fuſſeno egualmente obliqui ſotto a l’orizonte, ouer per il piano de l’orizonte, perche ſempre li dui angoli eſteriori ſaranno ſempre eguali, et li archi, ouer parte curue de quegli, ſempre ſaranno ſimile, perche le parti egualmente tolte de circonferentie de cerchi ſono ſimile et arguendo, come di ſopra e ſtato fatto ſe aprouara eſſer tal proportione della parte retta de l’uno alla parte retta de l’altro qual è della diſtantia de l’uno alla diſtantia de l’altro et de l’arco a l’arco, et per la premutata proportionalita ſe dimoſtrara eſſer tal proportione della parte retta de l’uno alla diſtantia del medemo ouer alla parte curua del medemo, qual ſara della parte retta del altro alla distantia, ouer alla parte curua di quello iſteſſo che ſara il propoſito. |
 the straight part AE has the same ratio to the straight part AH as the chord EF to the chord HI and as the distance AF to the distance AI and as the arc EF to the arc HI, which was to be shown. By means of the same methods and paths, the similarity of the transits, that is, of the violent motions, is also demonstrated when they are positioned in the same place below the horizon or along the plane of the horizon. [This happens because] the two external angles are always equal to each other and the arcs, that is, the curved parts of those [transits], are always similar to each other because if equal parts are taken away from circumferences of circles, these parts are similar. If one argues, as it has been done above, it can be confirmed that the straight part of one [transit] has the same ratio of the straight part of the one to the straight part of the other as the distance of the one to the distance of the other and as the arc to the arc. Due to the inverted ratio, it is demonstrated that the ratio the straight part of one [transit] has toward the length of the same [transit] or toward the curved part of the same, is the same ratio the straight part of the other [transit] has toward the length or toward the curved part of the other, which was to be shown. |
|
LIBRO SECONDO - 16v - cont. |
SECOND BOOK - 16v - cont. |
|
|
Propoſitione. VIII. Se una medema poſſanza mouente eiettara, ouer tirara corpi egualmente graui ſimili, et eguali in diuerſi modi |
Eighth proposition. If the same moving power ejects or throws equally heavy bodies, which are similar and equal to each other, violently through the air but in different manners,62 |
|
LIBRO SECONDO - 17r |
SECOND BOOK - 17r |
|
|
uiolentamente per aere, Quello che fara il ſuo tranſito eleuato a 45 gradi ſopra a l’orizonte fara ancora il ſuo effetto piu lontan dal ſuo principio ſopra il pian de l’orizonte che in qualunque altro modo eleuato. PEr dimoſtrare queſta propoſitione uſaremo una argumentation naturale la qual è questa, quella coſa che tranſiſſe dal minore al maggiore, et per tutti li mezzi, neceſſariamente tranſiſſe ancora per lo eguale, ouer queſt’altra. Doue accade trouar il maggiore, et ancora il minore di qualunque coſa, accade ancora retrouar lo eguale. Vero è che queſte tale argumentationi non ualeno, ne ſono accettate, ne conceſſe dal geometra, come euidentemente dimoſtra il comentatore ſopra la decimaquinta propoſitione del 3 de Euclide, et ſimelmente ſopra la trigeſima del medemo, nientedimeno tai concluſioni ſe uerifican in le coſe che ſono realmente uniuoce, ma in quelle che participano de equiuocatione, alle uolte ſono mendace, eßempi gratia che diceſſe el ſi troua vna portione di cerchio che ne da l’angolo constituido ſopra l’arco, menor del angolo retto e, queſta è la portione maggiore dil ſemicerchio (per la detta trigeſima del terzo di Euclide) ſimilmente el ſene troua un’altra che ne da il detto angolo maggior dil retto (et queſta è la portione minore dil ſemicerchio) [(]per la detta trigeſima del 3 di Euclide) adonque el ſaria poßibile per le dette argumentationi a trouarne una che ne dara il detto angolo eguale a l’angolo retto, hor dico che in queſto caſo la detta propoſitione, ouer argumentatione non ſara mendace, cioè che glie poßibile a trouar vna portione di cerchio, che ne dara realmente l’angolo conſtituido ſopra l’arco eguale a l’angolo retto, et queſto aduien perche nelli detti angoli non è alcuna equiuocatione. |
the one [equally heavy body] that accomplishes its transit at an elevation of 45 degrees above the horizon produces its effect farther away from its beginning and above the plane of the horizon than [if it were] elevated in any other way. To demonstrate this proposition, we use a natural argument, which is the following: that thing that transits from the smallest to the greatest and through all that is in-between necessarily transits through the equal.63 Or the following: if it happens to find the greatest and the smallest of any thing, it also happens to find the equal. It is true that this kind of argument is neither valid or accepted, nor conceded by the geometer, as is clearly demonstrated by the commentator64 on the fifteenth proposition of the third [book] of Euclid and, similarly, on the thirtieth [proposition] of the same [book]. Nevertheless, such conclusions are verified in [reference to] the things that are univocal in reality, but when they are ambiguous, such [arguments] are sometimes mendacious. For example, if I say that there is a portion of a circle65 whose angle composed on the arc is smaller than a right angle and that this portion is greater than the semicircle (because of the mentioned thirtieth [proposition] of the third [book] of Euclid), similarly another portion is found whose angle is greater than a right angle [(]and this portion is smaller than the semicircle) [(]because of the mentioned thirtieth [proposition] of the third [book] of Euclid). Then it is possible, based on the same [kind of] argument, to find a [portion] whose mentioned angle is equal to a right angle. In this case I say that the mentioned proposition, that is, argument, is not mendacious, which means that it is possible to find a real portion of circle whose angle composed on the arc is equal to a right angle. This happens because no ambiguity exists concerning the mentioned angles. |
|
LIBRO SECONDO - 17r - cont. |
SECOND BOOK - 17r - cont. |
|
|
Ma che diceſſe el ſi troua una portione di cerchio, che ne da l’angolo de detta portione menore de l’angolo retto (et queſta é la portion menore del ſemicerchio) [(]per la detta trigeſima del 3 di Euclide) Similmente el ſene truoua un’altra che ne da il detto angolo maggiore dil angolo retto (e queſta è la portione maggiore del ſemicerchio[)] (per la detta trigeſima del terzo) Adonque (per le dette argumentationi[)] el ſaria poßibile a trouarne una che ne deſſe il detto angolo eguale a l’angolo retto, hor dico che in queſto caſo la detta propoſitione, ouer argumentatione ſaria mendace perche l’angolo della portione dil cerchio non è realmente uniuoco con l’angolo retto perche l’angolo retto è contenuto da due linee rette, et l’angolo della portion è contenuto da una linea retta, et da una curua, cioè dalla corda et da l’arco di quella. Nondimeno dico che quella propoſitione, ouer argumentatione che è uera ſe uerifica sempre al senſo, et a l’intelletto in quella qualita media fra quelle due diuerſita, ouer qualita contrarie, cioe ſra la portion minore, et la portion maggiore, del ſemicerchio, la qual qualita media è propriamente eſſo ſemicerchio (come per la detta trigeſima del 3 de Euclide ſi proua) ma quella che mendace. Sempre ſe uerifica ancora lei in quanto al senſo pur in lo detto termine, ouer qualita media, cioè nel ſemicerchio, perche tal ſua mendacita non é ſenſibile, ne alcun senſo da ſe è atto |
But, I say that if there is a portion of a circle whose angle is smaller than a right angle66 (because this portion is smaller than the semicircle) [(]because of the mentioned thirtieth [proposition] of the third [book] of Euclid) and, similarly, if there is another [portion] whose angle is greater than a right angle (and this portion is greater than the semicircle[)] (because of the mentioned thirtieth [proposition] of the third [book]), then (because of the mentioned arguments[)] it is possible to find a [portion] whose angle is equal to a right angle. I say that in this case, the mentioned proposition, that is, argument, is mendacious because the angle of the portion of the circle is not unambiguous in reference to a right angle. For the right angle is composed of two straight lines, whereas the angle of the portion is composed of a straight line and a curved one, that is, by the chord and its arc. Nevertheless, I say that the proposition or argument, which is true, is always verified by the senses and by the intellect as the middle quality among those two diversities or contrary qualities. This means that, among the smaller and greater portion than the semicircle, the middle quality is exactly this semicircle (as is proved by the mentioned thirtieth [proposition] of the third [book] of Euclid). That [argument], which is mendacious, is also always verified by the senses in the same way as the middle quality, that is, as the semicircle. This is because its mendacity is not recognizable by the senses and none of the senses are appropriate to |
|
LIBRO SECONDO - 17v |
SECOND BOOK - 17v |
|
|
a conoſcerla in materia, ma ſolamente allo intelletto è nota, et ch’el ſia il uero el ſe ſa che l’angolo contenuto dalla corda, et da l’arco del ſemicerchio é tanto uicino a l’angolo retto che’l non è poßibile à coſtituir uno angolo acuto de linee rette che ſia piu uicino a l’angolo retto di lui, ne ancora tanto uicino quanto lui (come ſi proua ſopra la 15 del 3 de Euclide) ſeguita adonque che tai propoſitioni, ouer argumentationi ſempre ſe uerificano. In quanto al ſenſo in quel termine, ouer qualita media che giace fra due qualita contrarie in proprieta, ouer in effetti, cioè che egualmente participa di cadauna di quelle. Et per non ſtar in vn ſolo eßempio pigliamo queſt’altro. Il ſole girando continuamente per il zodiaco ne da alcune volte li giorni maggiori della notte, et alcune altre nelli da minori. Onde per le dette propoſitioni, ouer argumentationi ſeguiria che in alcun tempo, ouer luoco, ne doueſſe dar un giorno eguale alla notte, la qual coſa eßendo vera ſe uerificara al ſenſo, et all’intelletto in quello tempo, ouer in quel loco medio fra li dui tempi, ouer luochi maßimamente contrarij in tai effetti (li quai dui luochi maßimamente contrarij l’uno ſi è il primo grada de cancer, è l’altro ſi è il primo grado di capricorno, perche quando il ſole intra nel detto primo grado de cancer ne da il giorno piu longhißimo di la notte che in niun altro luoco, ouer tempo, et quando intra in el primo grado di capricorno ne da il giorno piu cortißimo di la notte, che in niun altro luoco. Ma il ponto medio fra questi dui eſtremi in effetto contrarij l’uno ſaria il primo grado di ariete e l’altro il primo grado de libra.) Ma ſe la detta argumentatione in queſto caſo ſara mendace. Dico che ſimilmente la ſe veriſicara ancora lei (in quanto al senſo) in li preditti luochi medij come continuamente uedemo che quando il ſole intra in vn di dui praeditti luochi il giorno ſe eguaglia alla notte, et ſe pur non ſe egualia perfettamente (come approua) et bene (il Reuerendiſſimo Cardinal Signor Pietro de Aliaco in la ſeſta queſtione ſopra Zuan di Sacrobuſto) tal differentia è inſenſibile. Hor tornando adonque al noſtro propoſito. Perche euidentemente ſapemo che ſe vn corpo egualmente graue ſara eietto, ouer tirato uiolentemente per il pian de l’orizonte quel andara a terminare il ſuo moto violente piu ſotto a l’orizonte che in qualunque modo eleuato, ma ſe lo andaremo elleuando pian piano ſopra a l’orizonte per vn tempo andara terminando il detto ſuo moto uiolente pur ſotto a l’orizonte, ma continuando tal eleuatione euidentemente ſapemo che a tempo terminara di ſopra al detto orizonte, et poi quanto piu ſe andara eleuando tanto piu andara a terminare piu in alto (ideſt piu lontano del detto orizonte) e |
recognize it in the materiality [of the things]. This can only be known by means of the intellect because it recognizes that the angle composed by the chord and by the arc of the semicircle is so similar to a right angle that it is not possible to compose an acute angle with two straight lines more similar to a right angle than the first one and neither as similar as the first one (as is proved using the fifteenth [proposition] of third [book] of Euclid). Therefore, it follows that such propositions or arguments are always verified by the senses in the same way, that is, [they are verified] as the middle quality among two contrary qualities and this [middle quality] has the same characteristics or effects of them, that is, it shares those [characteristics] equally with each of those [contrary qualities]. In order to have not only one example, we will furnish a second one. Revolving continuously along the Zodiac, the Sun sometimes makes days longer than nights and sometimes days shorter than nights. Therefore, based on the mentioned propositions or arguments, it follows that at a certain time or place, [the Sun] should be able to make a day that is equal to the night. If this is true, it can be verified by the senses and the intellect at that certain time or in that certain place which is in the middle of the two times or places that are maximally contrary to each other in reference to these effects (these two places, maximally contrary to each other, are the first degree of Cancer and the first degree of Capricorn. Because when the Sun enters the mentioned first degree of Cancer, it makes the longest day in comparison to the night than in any other place or time. When it enters the first degree of Capricorn, it creates the shortest day in comparison to the night than in any other place. The point that lies in between these two extremes and contrary effects is both the first degree of Aries and, the other the first degree of Libra). But, if the mentioned argument is mendacious, I say that it is nevertheless verified (concerning the senses) at the above-mentioned middle places as we constantly see that when the Sun enters one of the above-mentioned places, the day is equal to the night and, also if they are not perfectly equal to each other (as is proved by the Most Reverend Cardinal Lord Petrus Alliacus in the sixth question on Giovanni Sacrobosco), such a difference is not recognized by the senses. Now we will go back to what we want to show. We clearly know that if an equally heavy body is ejected or thrown violently along the plane of the horizon, it ends its violent motion at the lowest point below the horizon than [if it is] elevated in any other way. But, if we slowly elevate it above the horizon, for a while it will end its mentioned violent motion also below the horizon. But, if we keep increasing such elevation, we clearly know that at a certain point it will end above the mentioned horizon and the more it is elevated, the higher [above the plane of the horizon] it will end (that is, the farthest from the mentioned horizon). |
|
LIBRO SECONDO - 17v - cont. |
SECOND BOOK - 17v - cont. |
|
|
finalmente giongendo alla perpendicolare ſopra al orizonte (cioè che tal ſuo moto, ouer tranſito ſia retto ſopra a l’orizonte) quel terminara piu in alto ouer piu lontan di ſopra del detto piano del orizonte che in qualunque modo elleuato. Onde ſeguiria per le antedette propoſitioni, ouer argumentationi, che gli ſia una elleuatione coſi conditionata che’l debbia far terminare preciſamente in el proprio piano del orizonte, la qual argumentatione eſſendo vera ſe verificara realmente al ſenſo ancora al intelletto in quella eleuatione che è media fra quelle due maßimamente contrarie in terminatione (cioè fra quella che è per il piano del orizonte e quella che è retta ſopra al orizonte, perche l’una fa andare a terminare il detto |
Finally, once it arrives at the perpendicular above the horizon (so that its motion or transit is straight and at a right angle above the horizon), it ends at the highest and farthest [point] above the mentioned plane of the horizon than [if it is] elevated in any other way. From this and according to the above-mentioned propositions and arguments, it follows that there is an elevation characterized so that it ends precisely above the plane of the horizon.67 If this argument is true, it is verified in reality by the senses and also by the intellect at that elevation at the middle [point] of those two maximally contrary to each other concerning their ends (that is, the one that is along the plane of the horizon and the one directly above the horizon, because the first lets the mentioned |
|
LIBRO SECONDO - 18r |
SECOND BOOK - 18r |
|
|
corpo di moto uiolente piu di ſotto, et l’altra piu diſopra al orizonte, che in qualunque modo elleuato) et queſta eleuation media è quando il detto tranſito, ouer moto uiolente d’un corpo egualmente graue è elleuato alli 45 gradi ſopra al orizonte (cioe quando la parte retta di quello diuide l’angolo retto cauſato dalla perpendicolare ſopra al orizonte con el ſemidiametro del orizonte in due parti eguale) Ma ſe la detta argumentatione fuſſe mendace (per l’aduerſario geometrico) Se verificara pur ancora lei (in quanto al ſenſo) in la detta eleuation media, cioè alli 45 gradi ſopra a l’orizonte, ſe’l corpo adonque eietto, ouer tirato talmente che faccia il tranſito ſuo elleuato 45 gradi ſopra al orizonte, terminara il ſuo moto violente in el proprio pian del orizonte, et lo effetto che fara in el detto piano ſara il piu lontano dal ſuo principio (per la quarta suppoſitione) che far poſſa ſopra al pian del orizonte, in altro modo elleuato, eietto, ouer tirato dalla medema poſſanza che è il propoſito. Correlario. Da queſta propoſitione, et dalla ultima del primo, ſe manifeſta qualmente un corpo egualmente graue nel moto uiolente elleuato alli 45 gradi ſopra al orizonte fara menor effetto nel pian de l’orizonte che in qualunque altro modo elleuato. Propoſitione. IX. Se una medema poſſanza mouente eiettara, ouer tirara dui corpi egualmente graui ſimili, et eguali l’uno elleuato alli 45 gradi ſopra al orizonte, e l’altro per il pian del orizonte. La parte retta dil tranſito di quello che ſara elleuato alli 45 gradi ſopra al orizonte, ſara circa a quadrupla della parte retta di l’altro. |
body [that travels] with violent motion end at the lowest [point] and the other at the highest [point] in comparison to the horizon than [if it is] elevated in any other way). This middle elevation occurs when the mentioned transit or violent motion of an equally heavy body is elevated at 45 degrees above the horizon (that is, when its straight part divides the right angle, composed by the perpendicular above the horizon and the semidiameter of the horizon, into two equal parts). If the mentioned argument is mendacious (for the opposing geometer), it is still verified (in reference to the senses) at that mentioned middle elevation, that is, at 45 degrees above the horizon. Therefore, if the body is ejected or thrown so that it accomplishes its transit at an elevation of 45 degrees above the horizon, it ends its violent motion above its own plane of the horizon and the effect that it produces above the mentioned plane is the farthest away from its beginning (because of the fourth supposition) that it can produce above the plane of the horizon and than in any other way elevated, ejected or thrown by the same moving power, which was to be shown. Corollary. From this proposition and from the last of the first [book], it is manifest that an equally heavy body with a violent motion at an elevation of 45 degrees above the horizon produces a smaller effect above the plane of the horizon than [if it were] elevated in any other way. Ninth proposition. If the same moving power ejects or throws two equally heavy bodies similar and equal to each other, the first elevated at 45 degrees above the horizon and the other along the plane of the horizon, the straight part of the transit of the one elevated at 45 degrees above the horizon is about quadruple the straight part of the other. |
|
LIBRO SECONDO - 18r - cont. |
SECOND BOOK - 18r - cont. |
|
|
Per dimoſtrare queſta propoſitione, pigliaremo per ſuppoſito quello che in el principio diceßimo hauer trouato, cioè che la diſtantia dil tranſito, ouer moto uiolente elleuato alli 45 gradi ſopra a l’orizonte eſſer circa a decupla al tranſito retto, fatto per il pian del orizonte, che dal vulgo è detto tirar de ponto in bianco, la qual proportione ſe uedera coſi eſſere nel quarto libro doue ſe dara in numeri l’ordine, et la proportione di creſcer e calar di tiri de ogni ſorte machine. Sia adonque il ſemidiametro del orizonte la linea AB ella perpendicolar del detto orizonte la linea CAD et il tranſito d’un corpo egualmente graue fatto per il pian del orizonte la linea AEFG la parte retta dil quale ſia la linea AE et la curua la linea EF et il tranſito di moto natural la linea FG. Et il tranſito d’un altro corpo ſimile et egual al primo, e dalla medema poßanza tirato |
To demonstrate this proposition, we assume what we said to have found at the beginning, that is, that the distance68 of the transit or violent motion elevated at 45 degrees above the horizon is ten times the straight transit accomplished along the horizon, which is called shooting point blank in common parlance. This ratio is later shown to be true in the fourth book where the order and the ratios of the increasing and decreasing shots of each sort of machine are shown by means of numbers. Thus, let line AB be the semidiameter of the horizon and line CAD the perpendicular of the mentioned horizon. Let line AEFG be the transit of an equally heavy body accomplished along the plane of the horizon, whose straight part is the line AE and curved [part] the line EF and the transit of natural motion the line FG. Then, let there be the transit of the other body, similar and equal to the first, thrown by the same power. |
|
LIBRO SECONDO - 18v |
SECOND BOOK - 18v |
|
|
elleuato alli 45 gradi ſopra a l’orizonte, la linea AHIK la parte retta dil quale ſia la linea AH et la curua la linea HI tranſito di moto naturale la linea IK et la diſtantia la linea AEI la qual diſtantia uien a eſſer per il ſemidiametro del orizonte. Dico che la parte retta AH è circa a quadrupla della parte retta AE. Perche produro il tranſito naturale IK et la parte retta AH tanto che concorrano inſieme in ponto L et perche il ſemidiametro AB ſega orthogonalmente il tranſito naturale IK in ponto I (per la decimaottaua del 3 de Euclide) quel andaſſe per il centro dil cerchio donde deriua la parte curua HI. Compiro adonque (per la 24 del 3 di Euclide) il detto cerchio donde deriua la detta parte curua HI qual ſia HIMN et dal ponto A (per la 16 del 3 di Euclide) ducero una linea contingente al detto cerchio, quala pongo ſia AM et quella produro in diretto fin a tanto che la concorra con il tranſito natural IK in ponto O et ſara conſtituido il triangolo ALO hor dalli dui ponti H et M al centro del cerchio (qual pongo ſia P) duco le due linee HP et MP (le qual ſaranno eguale fra loro[)] (per la diffinitione dil cerchio poſta da Euclide nel I) Similmente la linea AH (per la 35 del terzo de Euclide) ſara eguale alla linea AM et l’angolo PHA ſara eguale a l’angolo PMA perche l’uno e l’altro e retto (per la 17 del 3 di Euclide) e la baſa AP è comuna a l’uno e l’altro di dui triangoli AHP et AMP onde (per la 8 del I de Euclide) li detti dui triangoli ſaranno equiangoli, et perche l’angolo HAP e mezzo angolo retto (per eſſer la mita de l’angolo CAP dal proſuppoſito) adunque l’angolo APH (per la 2 parte della 32 del I de Euclide) ſara ancora lui mezzo angolo retto. Seguita adonque, che l’angolo MAP de l’altro triangolo ſia ancora lui la mita d’un angolo retto, per il che tutto l’angolo HMA del triangolo ALO ſara retto, et perche langolo ALO è mezzo angolo retto (per eſſer eguale a l’angolo alterno LAC[)] (per la 29 del I de Euclide) Seguita (per la 2 parte della trigeſimaſeconda del I de Euclide) che l’altro angolo LOA ſia ancora lui mezzo angolo retto, onde (per la 6 del I de Euclide) lo lato AL ſara eguale al lato AO per il che tutto il detto triangolo ALO uien a eſſer mezzo un quadrato et la distantia AI uien a eſſer la perpendicolar del detto triangolo ALO ancora uien a eſſer egual alla mita della baſa LO cioe al LI |
elevated at 45 degrees above the horizon, AHIK, whose straight part is line AH, the curved [part] line HI and the transit of natural motion line IK. Let line AEI be the distance along the semidiameter of the horizon. I say that the straight part AH is about four times as long as the straight part AE. I prolong the natural transit IK and the straight part AH so that they meet at point L. Since the semidiameter AB orthogonally cuts the natural transit IK at point I (because of the eighteenth [proposition] of the third [book] of Euclid), it crosses the center of the circle, from which the curved part HI derives. I therefore draw (because of the twenty-fourth [proposition] of the third [book] of Euclid) the mentioned circle from which the curved part HI derives and this is HIMN. From point A (because of the sixteenth [proposition] of the third [book] of Euclid), I produce a line tangent to the mentioned circle, and this is AM. I then prolong this line so that it meets the natural transit IK at point O. As a result, the triangle ALO is produced. Now, from points H and M to the center of the circle (which I call P) I produce the two lines HP and MP (which are equal to each other[)] (because of the definition of the circle given by Euclid in the first [book]). Likewise, line AH (because of the thirty-fifth [proposition] of the third [book] of Euclid) is equal to line AM and angle PHA is equal to angle PMA, because both are right [angles] (because of the seventeenth [proposition] of the third [book] of Euclid). Since line AP is the common base to both triangles AHP and AMP, therefore (because of the eighth [proposition] of the first [book] of Euclid), the mentioned two triangles have the same angles. Because angle HAP is half of a right angle (because it is half of the angle CAP defined in the supposition), angle APH (because of the second part of the thirty-second [proposition] of the first [book] of Euclid) is therefore also half of a right angle. From this it follows that angle MAP of the other triangle is also half of a right angle and therefore the entire angle HAM of the triangle ALO is right. Since angle ALO is half of a right angle (because it is equal to the opposite angle LAC[)] and (because of the twenty-ninth [proposition] of the first [book] of Euclid), it follows (because of the second part of the thirty-second [proposition] of the first [book] of Euclid) that the other angle LOA is also half of a right angle. Therefore (because of the sixth [proposition] of the first [book] of Euclid), side AL is equal to side AO and thus the entire mentioned triangle ALO is half of a square and so the distance AI corresponds to the perpendicular of the mentioned triangle ALO and therefore it is also equal to half of the base LO, that is, to LI. |
|
LIBRO SECONDO - 18v - cont. |
SECOND BOOK - 18v - cont. |
|
|
et perche la detta distantia AI è ſuppoſta eſſer decupla alla retta AE cioe dieſe uolte tanto quanto è la retta AE onde larea del triangolo ALO (per la quadrageſimaprima del I de Euclide) ueneria a eſſer 100 cioè 100 quadrati della retta AE (la quale ſumemo in queſto loco per miſura di quello che ſe ha a dire) et lo lato AL ueria a eſſer la radice quadrata de 200 (per la penultima del I de Euclide) et ſimilmente l’altro lato AO. hor uolendo ſaper per numero la quantita della retta AH primamente del centro P duceremo le due linee PL et PO procederemo per algebra, ponendo che il ſemidiametro del cerchio ſia una coſa, et perche il detto ſemidiametro uien a eſſer la perpendicolar del triangolo PLO (ſopra la baſa LO) et ſimilmente del triangolo APL (ſopra la baſa AL) et ſimilmente del triangolo APO (ſopra la baſa AO) le quai perpendicolare ſono PI, PH et PM hor trouaremo l’area de cadauno di detti tre triangoli (per la ſua regola) multiplicando la perpendicolare contra la mita della baſa, ouer la mita della perpendicolar contra a tutta la baſa, onde multiplicando PI (che è poſto eſſer una coſa) fia la mita di LO che è 10 ſara 10 coſe per l’area |
Since the mentioned distance AI is assumed to be tenfold the straight line AE, that is, ten times the length of the straight line AE, the area of the triangle ALO (because of the forty-first [proposition] of the first [book] of Euclid) therefore becomes 100, that is, 100 squares of the straight line AE (which we assume here to be the fundamental measurement of what has to be demonstrated) and side AL corresponds to the square root of 200 (because of the penultimate [proposition] of the first [book] of Euclid) and similarly the other side AO. Now, if we want to know the measurement of the straight line AH by means of numbers, we first of all produce two lines PL and PO from the center P and then proceed algebraically. We assume that the semidiameter of the circle is one cosa.69 Since the mentioned semidiameter corresponds to the perpendicular of triangle PLO (to the base LO) and, likewise, of triangle APL (to the base AL) and, likewise, of triangle APO (to the base AO), and these perpendiculars are PI, PH and PM, we find the area of each of the mentioned three triangles (according to the appropriate rule) by multiplying the perpendicular with half of the base, or [by multiplying] half of the perpendicular with the entire base. Therefore, by multiplying PI (which is assumed to be one cosa) with half of LO, which is 10, it makes 10 cose for the area |
|
LIBRO SECONDO - 19v |
SECOND BOOK - 19v |
|
|
del triangolo PLO la qual ſaluaremo da parte, da poi multiplicaremo la perpendicolare PH (che è pur una coſa) fia la mita de AL che ſara Radice 50 ne uenira Radice de 50 cenſi (per l’area del triangolo APL[)] la qual poneremo da canto a preſſo di l’altra che ſaluaſſemo, da poi trouaremo ſimilmente l’area de l’altro triangolo APO la quale ſara pur la Radice de 50 cenſi ſi come fu di l’altro (perche le baſe ſono eguale, cioe che cadauna e Radice 200) hor ſumaremo inſieme queste tre aree, faranno in ſuma radice 200 cenſi piu 10 coſe, et queſta ſuma ſara eguale a l’area de tutto il triangolo ALO la qual è 100 onde leuando quella Radice de 20070 cenſi et restorando le parti et reccando a un cenſo haueremo vno cenſo piu 20 coſe egual a 100 onde ſeguendo il capitolo trouamo la coſa ualer Radice 200 men 10 et tanto fu lo ſemidiametro del cerchio, cioè la linea PH ouer PI ouer PM et perche la linea AH è eguale alla linea HP (come di ſopra fu dimoſtrato) ſeguita adonque che la detta linea AH ſia anchor lei Radice 200 men 10 il qual reſiduo ſaria circa 4
Correlario. Da queſto ſe manifeſta qualmente un corpo egualmente graue da una medema poſſanza eietto, ouer tirato uiolentemente per aere: ua piu per retta linea per un uerſo, che per un altro, et conſequentemente fa maggior effetto. FINE DEL SECONDO LIBRO. |
of triangle PLO, and we set this result aside. Then, we multiply the perpendicular PH (which is also [equal] to one cosa) with half of AL, which is the square root of 50. It makes the square root of 50 censi71 (for the area of triangle APL[)], which we set aside together with the other that we have already set aside. Then similarly, we find the area of the other triangle APO, which is also the square root of 50 censi, like the result of the other (because the bases are equal to each other, that is, both are square roots of 200). Now we sum up these three areas and these results into the square root of 200 censi plus 10 cose. This sum is equal to the area of the entire triangle ALO, which is 100. Therefore, by raising the square root of 200 censi,72 by rounding the parts73 and reducing them to one censo, we have one censo plus 20 cose equal to 100. By following the procedure, we therefore find that one cosa is the square root of 200 minus 10 and this is the semidiameter of the circle, that is, line PH, PI or PM. Since line AH is equal to line HP (as demonstrated above), it follows that the mentioned line AH is also the square root of 200 minus 10 and the result of this is about 4
Corollary. From this, it is manifested that an equally heavy body ejected or thrown violently through the air by the same power moves farther along a straight line in one direction than in another and, therefore, it produces a greater effect. END OF THE SECOND BOOK. |
|
LIBRO TERZO - 20r |
THIRD BOOK - 20r |
|
|
Third Book COMINCIA IL TERZO LIBRO DELLA NOVA SCIENTIA DI NICOLO TARTAGLIA BRISCIANO. Diffinitione. Prima. ORizonte (in queſto luoco) è detto quel piano circolare che diuide (non ſolamente) lo hemiſperio inferiore dal ſuperiore, ma anchor a locchio riſguardante alcuna coſa apparente in due parti eguali, et è concentrico con quello. Diffinitione. II. Perfetto piano ſe chiama qualunque ſpacio terreo, che procede, ouer che ſe iſtende egualmente diſtante al pian de l’orizonte, di ſotto a eſſo orizonte. Diffinitione. III. L’altezza delle coſe apparente é la perpendicolare dutta dalla uertice di cadauna di quelle, alla baſa, ouer piano terreo doue eſſe ſe ripoſſano. Diffinitione. IIII. Diſtantia ipothumiſſale, ouer diametrale, è quella, che è per retta linea dal occhio riſguardante, alla uertice di qualunque altezza apparente[.] Diffinitione. V. Diſtantia orizontale è quella che è per retta linea dal occhio riſguardante, a alcuna coſa apparente che ſia in el pian del orizonte. |
THE THIRD BOOK OF THE NOVA SCIENTIA OF NICOLÒ TARTAGLIA STARTS. First definition. The horizon (in this place) is said to be the circular plane which (not only) divides the hemispheres into the lower and upper ones, but also the eye while targeting a certain perceptible object. This eye is divided into two equal parts and is also concentric to the horizon. Second definition. A perfect plane is said to be whichever terrestrial space that expands or extends equally far from the plane of the horizon and also below the same horizon. Third definition. The height of perceptible objects is the perpendicular line drawn from the highest point of each object to its base or to the terrestrial plane on which the object stands. Fourth definition. The diametral distance, or hypotenuse, is that which connects, by means of a straight line, the observing eye with the vertex of whichever perceptible height. Fifth definition. The horizontal distance is that which connects, by means of a straight line, the eye to whichever perceptible object that is above the plane of the horizon. |
|
LIBRO TERZO - 20v |
THIRD BOOK - 20v |
|
|
Propoſitione. Prima. Mi uoglio certificare in materia ſe una data regola (ouer Rega) materiale per deſignar linee rette è giuſta. SIa la data Regola, ouer Rega A della quale mi uoglio certificare ſella è giuſta per tirare et deſignare artificialmente linee rette in ogni piana ſuperficie, ſegno li dui ponti B et C picolini quanto ſia poßibile luntani luno da laltro circa a tanto quanto è longa la data Regola, ouer Rega A come nel primo eſſempio appare, da poi acontio, ouer giuſto la data Regola alli detti dui ponti ſtante il corpo della detta regola verſo mi, come nel ſecondo eſſempio ſi uede, dapoi dal ponto A al ponto B tiro leggiermente una linea ſuttiliſſima ſecondo l’ordine della data regola, fatto queſto uolto la data regola da laltra banda della tirata linea, giuſtandola diligentemente alli detti dui ponti, come nel terzo eſſempio appare, et tiro leggiermente un’altra linea dal detto ponto A al ponto B ſutilißima  fatto queſto leuo la detta regola, ouer rega et guardo diligentemente ſe la linea tirata a queſta ſeconda uolta congruiſſe perfettamente ſopra a quella, che fu tirata alla prima, cioe che la ſia in quella iſteſſa, la qual coſa eſſendo coſi diro, che la detta regola, ouer rega è giuſtißima, ma quando che la linea tirata la ſeconda uolta non congrueſſe perfettamente ſopra a quella, che fu tirata prima, et che fra l’una è l’altra ſeraſſeno qualche ſpacio, come in lo quarto eſſempio appare, a l’hor diro che tal regola in modo alcuno non è giuſta, ne le linee ſignate, ouer tirate ſecondo l’ordine di quella non ſono rette, perche due linee rette non pono ſra l’una et l’altra ſerare alcuna ſuperficie (per la ultima petitione del primo di Euclide) che è il propoſito. |
First proposition. I would like to deepen the subject matter of whether a given material ruler for drawing straight lines is built properly. Let there be a ruler A with which I would like to verify whether it is appropriate to artificially draw lines that are straight on every plane surface. I draw two points B and C as small as possible and distant from each other almost as much as the length of the given ruler A, as is shown in the first example. Then I position the ruler as close as possible to the points keeping the ruler on my side, as is shown in the second example. Afterward, I draw a very thin faint line from point A to point B following the side of the ruler. Once this is done, I turn the ruler on the other side of the drawn line and I diligently position it as close as possible to the two points, as appears in the third example. Then I draw another very thin faint line from the mentioned point A to point B.  Once this is done, I take away the mentioned ruler and I diligently observe whether the second line is exactly on the first one or, in other terms, whether it stays within that one. If this is the case, I will say that the mentioned ruler is very accurate. But, if the second line is not exactly on the first and if there is some space between the first and the second line, as appears in the fourth example, I will say that this ruler is not accurate and that the lines drawn according to its sides are not straight, because two straight lines cannot have any space between each other (based on the last postulate of the first [book] of Euclid). This was our purpose. |
|
LIBRO TERZO - 21r |
THIRD BOOK - 21r |
|
|
Propoſitione. II. Mi uoglio certificare in materia ſe una propoſta ſquara materiale e giuſta. SIa la detta ſquara A. Dico che mi uoglio certificare s’ella è giuſta, et ſe li angoli deſignati ſecondo l’ordine di quella ſono perfettamente retti, faccio in queſto modo, deſegno l’angolo BCD ſecondo l’ordine della detta ſquara,  poi piglio un compaßo, et faccio centro il ponto C et ſopra quello deſcriuo il cerchio EFG maggior che ſia poßibile pur che non tranſiſca fuora delle due linee CB et CD ma che ſeghi cadauna di quelle in li dui ponti EF fatto questo, piglio il mio compaßo, et con diligentia guardo ſe l’arco FE è preciſamente il quarto della circonferentia di tutto il detto cerchio, la qual coſa eßendo coſi, diro che il detto angolo C è perfettamente retto (per la 2 propoſitione del 2) e conſequentemente la ſquara A eßer giusta (per la ottaua comuna ſententia del primo di Euclide) ma ſe il detto arco FE ſara piu, ouer meno della quarta parte della circonferentia del detto cerchio, diro che il detto angolo C in conto alcuno non é retto è conſequentemente la detta ſquara A non eßer giusta. Propoſitione. III. Per un altro modo (per eſſer piu ſicuro) mi uoglio certificare in materia ſe la data ſquara e giuſta. |
Second proposition. I would like to deepen the subject matter of whether a material set square is correct. Let there be the mentioned set square A. I say that I would like to verify whether it is correct and if the angles designed in it are perfectly right too. I do this in the following way. I draw the angle BCD according to the sides of the mentioned set square.  Then I take a compass and I draw, with point C at the center, the circle EFG as large as possible but I avoid drawing outside the lines CB and CD. Instead, the circle has to meet these lines at points E and F. Once this is done, I take my compass and I check whether arc FE is exactly one fourth of the circumference of the mentioned entire circle. If this is the case, I will say that the mentioned angle C is perfectly right (based on the second proposition of the second [book]) and, consequently, that the set square A is correct (based on the eighth common sentence [axiom] of the first [book] of Euclid). But, if the mentioned arc FE is longer or shorter than the fourth part of the circumference of the mentioned circle, I will say that the mentioned angle C cannot be right and therefore the mentioned set square is not correct. Third proposition. I would like to verify by means of another method (in order to be more certain) in reference to the subject matter of whether the given set square is correct. |
|
LIBRO TERZO - 21v |
THIRD BOOK - 21v |
|
|
SIa la data ſquara A. Dico, che per eſſer piu ſicuro mi uoglio per un’altro modo certificare ſe quella e giuſta, deſegno l’angolo BCD ſecondo l’ordine di quella, poi dal ponto B al ponto D tiro la linea BD et quella diuido in due parti eguali in ponto E elqual ponto E faccio centro, et ſopra di quello deſcriuo un ſemicerchio  ſecondo la quantita della linea EB ouer ED qual ſia BFGD fatto queſto guardo diligentemente, ſe la detta circonferentia BFGD andaſſe apponto per il ponto C la qual coſa, eſſendo coſi, diro che il detto angolo C (per la 30 del terzo di Euclide) è perfettamente retto et conſequentemente la data ſquara A eſſer giuſta, ma ſe la detta circonferentia andaſſe quanto piu di ſopra, ouer di ſotto dal detto ponto C diro abſolutamente, che il detto angolo C non é retto e conſequentemente la ſquara A non eſſer giuſta, che è il propoſito. |
Let there be the set square A. I say that in order to be more certain, I would like to verify whether it is correct by means of another method. I draw the angle BCD according to its sides and then I draw the line BD from point B to point D. I then divide this line into two equal parts at point E. Taking this point E as a center I draw a semicircle  taking line EB or ED as the opening [of the compass]. The semicircle will be BFGD. Once this is done, I diligently observe whether the mentioned circumference BFGD meets point C exactly. If this is the case, I say that the mentioned angle C (because of the thirtieth [proposition] of the third [book] of Euclid) is perfectly right and, consequently, the given set square A is correct. But, if the mentioned circumference runs either a little above or a little below the mentioned point C, then I resolutely say that the mentioned angle C is not right and, consequently, that the set square A is not correct. This was to be shown. |
|
LIBRO TERZO - 21v - cont. |
THIRD BOOK - 21v - cont. |
|
|
Propoſitione. IIII. Anchora per un’altro modo mi uoglio certificare in materia ſe la data ſquara è giuſta. SIa la data ſquara A. Dico ancora (per eſſer piu ſicuro) mi uoglio per un’altro modo uerificare ſe quella è giuſta deſcriuo l’angolo BCD ſecondo l’ordine di quella fatto questo piglio il mio compaſſo, et appro quello talmente che la appritura poſcia intrare tre uolte in la linea CD [(]uel circa) et ſecondo la detta appritura aſſegno le tre parti CE, [E]F et FG et ſecondo la medema appritura di compaſſo aſſegno in l’altra linea CB le quatro parti, ouer miſure CH, HI, IK, KL fatto queſto dal ponto L al ponto G tiro la linea LG poi con diligentia guardo ſe la detta |
Fourth proposition. I would like to reverify the subject matter of whether the set square is correct by means of another method. Let there be the set square A. I say once more (in order to be more certain) that I would like to verify whether the set square is correct by means of another method. I draw the angle BCD according to its sides. Once this is done, I take the compass and open it in such a way that its opening is set to be one third of the line CD [(]or almost). According to this opening, I mark the three segments CE, [E]F74 and FG. Then, keeping the same opening of the compass, I mark the four segments or distances CH, HI, IK, KL on the other line CB. Once this is done, I draw the line LG from point L to point G. Then, I diligently observe whether the mentioned |
|
LIBRO TERZO - 22r |
THIRD BOOK - 22r |
|
 linea LG è preciſamente cinque miſure, ouer appriture del detto mio compaſſo, la qual coſa eſſendo coſi, diro che il detto angolo C (per la ultima del primo di Euclide) è perfettamente retto, et conſequentemente la ſquara A eſſer giuſta, ma ſe la detta linea LG ſara piu, ouer manco de cinque appriture del detto mio compaſſo, diro abſolutamente che il detto angolo C non eſſer retto e conſequentemente la ſquara A non eſſer giuſta, che è il propoſito. Propoſitione. V. Mi uoglio certificare in materia ſe un dato quadrangolo equilatero e perfetto quadro. SIa il quadrangolo ABCD equilatero, cioe che li quatro lati AB, BC, CD et DA ſiano eguali, dico che mi uoglio certificare ſe il detto quadrangolo è perfetto quadro, tiro in quello li dui diametri AC et BD li quali ſe interſegano in ponto E poi piglio il mio compaſſo, et faccio il ponto E centro, et deſcriuo un cerchio ſecondo la quantita de EA ouer de EB da poi con diligentia guardo ſe la circonferentia del detto cerchio andaſſe preciſamente per le quatro iſtremita di quatro angoli A, B, C, D del detto quadrangolo, et ſe la detta circonferentia andara pontalmente per le dette iſtremita diro, che il detto quadrangolo (per la 30 del terzo de Euclide) ſara rettangolo, et conſequentemente perfetto quadro. Ma ſe per caſo la detta circonferentia non andara pontalmente per tutte le dette quatro iſtremita, diro abſolutamente, che il detto quadrangolo non eſſer rettangolo, et conſequentemente quel non eſſer perfetto quadro, che è il propoſito. |
 line LG is precisely as long as five such distances or openings of the mentioned compass of mine. If this is the case, I will say that the mentioned angle C (based on the last [proposition] of the first [book] of Euclid) is perfectly right and, consequently, the set square A is correct. But, if the mentioned line LG is longer or shorter than the five openings of the mentioned compass of mine, I will resolutely say that the mentioned angle C is not right and, consequently, that the set square A is not correct. This was to be shown. Fifth proposition. I would like to verify the subject matter of whether an equilateral quadrangle is perfectly square. Let the quadrangle ABCD be equilateral, namely with four equal sides AB, BC, CD and DA. I say that I would like to verify whether the mentioned quadrangle is perfectly square. Inside this square, I draw the two [diagonals] AC and BD, which meet at point E. Then I take my compass and, with point E as the center, I draw a circle according to the distance EA or EB. Then, I diligently observe whether the circumference of the mentioned circle precisely meets the four extremities of the four angles A, B, C, D of the mentioned quadrangle. If the mentioned circumference precisely meets those mentioned points, I will say that the mentioned quadrangle (based on the thirtieth [proposition] of the third [book] of Euclid) is rectangular and, consequently, perfectly square. But, if it happens that the mentioned circumference does not precisely meet the mentioned four extremities, I will resolutely say that the mentioned quadrangle is not rectangular and, consequently, not perfectly square. This was to be shown. |
|
LIBRO TERZO - 22v |
THIRD BOOK - 22v |
|
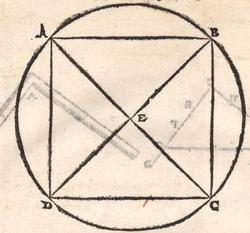 Propoſitione. VI. Mi uoglio fabricar uno iſtrumento che mi ſerua a liuelar un piano, et ancora a conoſcerlo con laſpetto, le altezze, larghezze profundita, diſtantie hipotumiſſale, et horizontale delle coſe apparente, et che ancora con facilita me lo poſſa accomodar da inueſtigar la uarieta di tiri de cadauno pezzo de artegliaria, et ſimilmente de ogni mortaro. |
 Sixth proposition. I would like to manufacture an instrument for myself that I can use to level the ground and to analyze it by sight and [to measure] the heights, widths, depths, and diametral and horizontal distances of perceptible objects. This instrument should also be easily usable to investigate the variety of shots75 of each piece of artillery and, similarly, of each mortar. |
|
LIBRO TERZO - 22v - cont. |
THIRD BOOK - 22v - cont. |
|
|
Piglio una lamina di alcun metallo ben piana groſſa una bona coſta di cortello, ouer una tauoletta di alcun legno ſodo e ben ſecco groſſa al men un dedo groſſo, et con una rega, et ſquadra giusta, ne cauo della detta lamina, ouer tauoletta una ſquadra alla ſimilitudine della infraſcritta ABC, DEF che habbia interchiuſo uno perfettißimo quadro alla ſimilitudine del quadro EGHI et luntano una coſta di cortello, uel circa da li dui lati GH et HI tiro tre linee luntane l’una da l’altra un dedo groſſo, uel circa equidiſtante alli detti dui lati GH et HI et cadauna di quelle due che ſono propinque alli detti dui lati HG et HI diuido in 12 parti eguali et dal angolo E a cadauno delli detti 12 e 12 diuiſioni, ouer ponti, tiro le linee diuidente li ſpaci, che interchiude le tre, e tre linee equidistanti alli dui lati GH et HI in 12 ſpaci eguali, et coſi haro compita la figura gnomonica KHL diuiſa in 12 e 12 parti eguali, la qual figura dalli antiqui e chiamata ſchala altimetria, et la parte HL é detta ombra retta, et la parte HK e chiamata ombra uerſa, et la linea HE (cioé il diametro del quadro) é detta linea de l’ombra media, et la diuiſione I de l’ombra retta ſe chiama il primo ponto |
I take a foil of a certain metal, flat and as wide as the blade of a knife, or I take a wooden board, hard and thoroughly dried and as wide as a thumb. By means of a correct ruler and a correct set square, I produce, from the mentioned metal foil or board, a set square that looks like the drawn one ABC, DEF and contains a very perfect quadrant that looks like the quadrant EGHI. Within the space of the width of a blade of a knife, close to the two sides GH and HI, I draw three lines the space of a thumb distant from each other and equidistant from the mentioned sides GH and HI. I divide each of the two lines, which are closer to the mentioned sides GH and HI, into twelve equal parts and then I draw lines from angle E to each of these twelve and to twelve segments, or points. These lines divide the spaces that contain the [first] and the other three lines, which are equidistant from sides GH and HI, into twelve equal spaces.76 In this way, the gnomonic figure KHL is accomplished and is divided into twelve and into another twelve equal parts. This figure was called altimetric scale by the ancients. Side HL is called the vertical shadow and side HK is called the horizontal shadow. Line HE (that is, the diameter of the quadrant) is called middle line of the shadow. Portion 1 of the vertical shadow is called the first point |
|
LIBRO TERZO - 23r |
THIRD BOOK - 23r |
|
 della ombra retta, et la diuiſione 2 il ſecondo ponto, et coſi diſcorrendo nelle altre diuiſioni della ombra retta e ſimilmente la diuiſione prima della ombra uerſa ſe dice il primo ponto della ombra uerſa e coſi la diuiſione 2 ſe dice il ſecondo ponto della ombra uerſa, et coſi diſcorrendo nelle altre diuiſioni. Hor per compir questo noſtro istromento ſopra la gamba BC de fuorauia aſſettaro le due laminette preforate M, N talmente che li dui forami ſiano in retta linea ancora egualmente diſtanti dal piano BC et faro li detti forami picoli che apena il raggio uiſuale gli poſſa andare, et per quelli ueder la ſumita delle coſe apparente, da poi fiſſaro un ferretto perpendicolarmente in ponto E et a quello gli atacaro il perpendicolo, ouer piombino EO et ſara compito il detto iſtromento che è il propoſito. |
 of the vertical shadow and portion 2 is the second point and so it can be continued concerning the other portions of the vertical shadow. Similarly, the first portion of the horizontal shadow is called the first point of the horizontal shadow, and this, the second portion, is called the second point of the horizontal shadow and so it can be continued concerning the other portions. Now, in order to accomplish the building of our instrument, I will assemble on the external side of the leg BC two perforated small foils M and N in such a way that the two holes are on a straight line always equally distant from plane BC. I will make the holes just small enough to allow a visual ray to pass through so that the top of the perceptible objects can be seen. Then, I fix a small piece of iron perpendicularly at point E and will hang the plumb line EO from it. The instrument will then be completed. This was to be shown. |
|
LIBRO TERZO - 23r - cont. |
THIRD BOOK - 23r - cont. |
|
|
Correttione del Authore. CIaſcaduna coſa da poi, che è fatta, ſe la fuſſe da fare molto meglio ſe faria, e per tanto dico che in luoco di quelle due laminette preforate M et N molto piu iuſtamente reſpondera, et ſeruira facendo fare uno canaletto picollino, con un pi[r]on[c]ino, accio atto, nella banda de ſotto della gamba FB qual uada rettamente dal ponto F al ponto P et questo ſi debbe fare auanti che ſia incolato la detta gamba FB ſopra il quadrato GHIE et dapoi fatto il detto canaletto incollar la detta gamba al ſuo luoco, et da poi incollar una liſtetina ſottila del medeſimo legno, nella |
Correction of the author.77 If then each thing that has been made has to be made even better, I say that instead of those small perforated foils M and N, it would work more precisely if a small pipe were made with a very small pivot, and therefore apt to be fixed on the internal side of the leg FB and in a way that goes straight from point F to point P. This should be accomplished before the leg FB is glued on to the quadrant GHIE. Once the mentioned small pipe is glued on to the mentioned leg at its proper place, a small and thin strip of the same wood is glued over |
|
LIBRO TERZO - 23v |
THIRD BOOK - 23v |
|
|
parte IF per couerzer quella parte del detto canaletto che iui ſera, el qual canaletto perche uenira a paſſare rettamente ſotto al centro E doue ua attacato il perpendicolo, ouer piombino, molto piu iuſtamente ne ſeruira nelle nostre operationi, di quello fara le dette due laminette, come detto diſopra, et maßime doue biſogna traſportar liſtrumento da un luoco in un’altro, come occorre nella decima propoſitione di queſto. Anchor biſogna notar, che uolendo far queſta ſquadra de legno, la ſi debbe far di legno di ancipreſſo a tento, che ho ritrouato quello non far mai ſenſibile mutatione, ne per humidita ne per ſcicita, et dapoi deſignar la detta ſquadra in carta, et incollarla ſopra a quella di legno. Oltra di queſto biſogna notare, che quanto piu ſara maggiore queſto iſtromento, tanto piu ſara atto a dar la coſa piu giuſta, et in uero il quadrato GHIE non uoria eſſer men di una ſpanna per lato, talmente che cadauno delli detti 12 et 12 ponti della ombra retta, et uerſa ſe poßino diuidere in altre 12 et 12 parti ſecondo il medeſimo modo le quai parti ſe chiamariano minuti, tal che il detto quadro ueria a eßer poi 144 minuti per fazza, li quali ſeruiranno molto piu pontalmente, et ſottilmente di quello faria ſolamente con le 12 prime diuiſioni. Propoſitione. VII. Voglio liuelar un ſpacio terreo, et conoſcer ſe quello e perfetto piano. SIa il ſpatio terreo la linea AB. Dico che uoglio liuellar il detto ſpacio, et certificarme ſe eglie perfetto piano, apoſto un ponto in qualche coſa elleuata perpendicolarmente ſopra il pian del orizonte, et ſia il ponto C poi piglio il 
|
part IF of the mentioned small pipe so that the pipe will remain straight below the center and the plumb line will hang. This construction allows more precision in our operations than the above-mentioned solution of the two small foils, especially if there is the need to transport the instrument from one place to another, as will be described in the tenth proposition of this work. It should also be noted that if the instrument is made of wood, then cypress wood should be used because it does not change due to humidity or dryness, as I found. In this case, the mentioned set square is drawn on paper and then glued on to the wooden square. Moreover, it has to be noted that the larger the instrument, the more precisely it operates. The side of the quadrant GHIE should not be smaller than a span so that each of the mentioned twelve, and the other twelve points of the vertical shadow and of the horizontal shadow can be divided into a further twelve and twelve portions according to the same method. These smaller portions are called minutes and the mentioned quadrant would be divided into 144 minutes on each side. This solution offers higher precision than the one reached using only twelve portions. Seventh proposition. I would like to level the ground and know whether it is perfectly flat. Let the line AB be the ground. I say that I would like to level the mentioned space and verify whether it is perfectly flat. I take a point over an object that is elevated perpendicularly over the plane of the horizon. Let this point be C. I then take 
|
|
LIBRO TERZO - 24r |
THIRD BOOK - 24r |
|
|
mio istromento, et lo aſſetto, ouer acconcio fißamente in qualche coſa ſtabile talmente che lo perpendicolo EO cada preciſamente ſopra il lato EG del quadrato, cioe ſopra la linea EGD et poi lo alzo ouer abbaßo, talmente che per li forami MN ueda il ponto C ſatto queſto, miſuro diligentemente quanto è dal mio occhio, ouer dal forame N perpendicolarmente in terra (cioè quanto é la linea NA) et ſimilmente miſuro quanto è dal ponto C perpendicolarmente a terra (cioè quanto è la linea CB[)] et ſe trouo che la detta linea CB ſia eguale al la linea NA et che il detto piano ſe distenda dalla banda deſtra, et dalla ſiniſtra ſecondo l’ordine della linea AB diro che il detto piano AB ſara perfetto piano, perche la linea AB che andaße per quello (per la trigeſimaterza del primo di Euclide) ſara equidiſtante alla linea NC che andaße per il piano de lorizonte, conſequentemente il detto piano donde andaße la detta linea AB ſara equidiſtante (per la decimaquarta del II di Euclide) al pian del orizonte, ma ſe la linea CB ſara maggiore della linea NA diro che il detto piano terreo ſara piu baßo uerſo B che uerſo A et è conuerſo, ſe la linea CB ſara minore della linea NA diro che il detto piano terreo ſara piu alto uerſo B che uerſo A et con lo medemo ordine procedero dalla banda deſtra, et dalla ſinistra uolendome certificare ſe circum circa ſe iſtende ſecondo la detta linea AB che è il propoſito. Propoſitione. VIII. Voglio inueſtigare l’altezza de una coſa apparente, alla qual ſi poſci andare alla baſa, ouer fondamento di quella, et tutto a un tempo uoglio comprehendere la diſtantia ypothumiſſale, ouer diametrale di tal altezza. |
my instrument78 and position it or fix it stably over something so that the plumb line EO falls precisely over side EG of the quadrant, that is, over line EGD. I then lift it up or lower it to be able to see point C through the holes M and N. Once this is done, I diligently measure the distance between my eye, or the hole N, and the point where the perpendicular line from N meets the ground (that is, the length of the line NA). Similarly, I measure the distance between point C and the point of the perpendicular line from this point and the ground (that is, the length of the line CB[)]. Thus, if I find that the mentioned line CB is equal to the line NA and that the mentioned ground extends on the right and left sides according to the line AB, I say that the mentioned ground AB is perfectly flat. This is because the line AB that lies on the ground (based on the thirty-third [proposition] of the first [book] of Euclid) is equidistant to the line NC that lies over the plane of the horizon. Consequently, the mentioned ground through which line AB passes is equidistant (based on the fourteenth [proposition] of the eleventh [book] of Euclid) to the plane of the horizon. But if line CB is longer than line NA, I will say that the mentioned ground is lower toward B than toward A and, conversely, if line CB is shorter than line NA, I will say that the mentioned ground is higher toward B than toward A. According to the same method, I would then go ahead on the right and left sides if I want to verify whether the ground around it extends according the mentioned line AB. This was to be shown. Eighth proposition. I would like to find the height of a perceptible object, toward whose lowest part or fundament one can move and, using the same operation, I would like to know the hypotenuse or diametral distance of such a height. |
|
LIBRO TERZO - 24r - cont. |
THIRD BOOK - 24r - cont. |
|
|
SIa l’altezza AB della coſa apparente A elleuata, et coſtituta ſopra il piano terreo BD talmente che ſi poſcia andare alla baſa, ouer fondamento di quella (cioè al ponto B). Dico che uoglio inuestigare la detta altezza AB et tutto a un tempo uoglio conprehendere la distantia ypothumißale, ouer diametrale di tal altezza. Piglio il mio iſtromento, et affißo quello in qualche coſa ſtabile, et liuello il piano BD et uedo ſi glie perfetto piano (procedendo, come nella paßata fu fatto) et ſe lo trouo perfetto piano mi appoſto un ponto in la detta coſa apparente qual ſia la uertice A et quella cerco de uedere per li dui forami N, M del mio iſtromento, et mi uado tirando tanto in drio, ouer auanti che il perpendicolo cada ſopra la linea della ombra media, cioè ſopra il diametro del quadro come di ſotto appar in figura, fatto queſto miſuro il ſpacio che è dal ponto doue cade la perpendicolar del mio occhio fina alla baſa de tal altezza (cioè quanto è dal ponto C al ponto B) et a quella quantita gli agiongo la perpendicolare, che è dal mio occhio a terra (cioè la quantita EC) e tanto quanto ſara queſta ſuma tanto ſara anchora l’altezza AB. Eßempi gratia, ſe il ſpacio CB fuße paßa 353 et che dal occhio mio a terra (cioe dal ponto E al ponto C[)] fuße paßa dui |
Let there be height AB of the perceptible object A that is elevated and conceived of over the ground BD so that one can move to its lowest part or fundament (that is, to point B). I say that I would like to know the mentioned height AB and, with the same operation, to know the hypotenuse or diametral distance of that height. I take my instrument79 and I fix it onto something stable. I level the ground BD and check whether it is perfectly flat (using the method described previously).80 If I find that the ground is perfectly flat, I then target a point of the mentioned perceptible object, for instance, point A at its top, and I try to see it through the two holes N and M of my instrument. I move backward or forward up to the point where the plumb line is exactly over the middle line of the shadow, that is, over the diameter of the quadrant as is shown in the figure below. Once this is done, I measure the space between the point where the perpendicular from my eye and the ground falls, and the point at the fundament of the height to be known (that is, the length from point C to point B). To this quantity I add the length of the perpendicular between my eye and the point where the perpendicular from my eye falls to the ground (that is, the quantity EC). The result of this sum will be the measurement of height AB. For example, if space CB is 353 steps long and the space from my eye to the ground (that is, from point E to point C[)] is two steps long, |
|
LIBRO TERZO - 24v |
THIRD BOOK - 24v |
|
|
conchiuderei che la altezza AB fuſſe paſſa 355. Perche dal occhio mio (cioè dal ponto E) duco la linea EF equidiſtante al piano, ouer linea CB et produco il perpendicolo del mio iſtromento fin a tanto che quel concorra con la linea uiſuale, EA in ponto H et produco ſimilmente lo lato della ombra retta, cioè la linea GI (lato del quadro) fin a tanto che concorra con la medema linea uiſuale EA in ponto K cauſando il triangolo GKH et perche l’angolo GKH è eguale (per la terza petitione del primo di Euclide) a l’angolo EFA (perche l’uno e l’altro è retto) et ſimilmente l’angolo KHG è eguale (per la ſeconda parte della 29 del primo di Euclide) a l’angolo EAF onde (per la ſeconda parte della trigeſima [seconda] del I di Euclide) l’angolo KGH uerria a reſtar eguale a l’angolo AEF per il che il triangolo GKH uerria a eſſer equiangolo con il triangolo EAF et conſequentemente ſimile et de lati proportionali (per la quarta dil ſeſto di Euclide) et perche il triangolo GIL verria a eſſer ſimile al triangolo GKH (per la 2 del ſeſto di Euclide) ancora il triangolo EAF (per la uigeſima del ſeſto di Euclide) uerra a eſſer ſimile al detto triangolo GLI et de lati proportionali adonque tal proportione ha il lato EF al lato FA qual ha il lato GI al lato IL et perche il lato IL è eguale al lato IG (per eſſer cadaun lato del quadrato) il lato adonque AF ſara eguale al lato EF et perche il ſpacio, ouer linea CB (per la trigeſimaquarta del I di Euclide) è eguale al medemo lato EF ſeguita (per la prima comuna ſententia del I di Euclide) che la partial altezza AF ſia eguale alla diſtantia, ouer linea CB et perche lo reſiduo FB (di tal altezza) è eguale (per la detta trigeſimaquarta del I di Euclide) alla linea EC ſeguita adonque (per la ſeconda comuna ſententia del I di Euclide) che la quantita BC gionta con la quantita CE tal ſuma ſara eguale a tutta l’altezza AB che è il primo propoſito. Et perche ſi come il lato GI al lato GH (diametro del quadro) coſi è il lato EF (ouer CB) al lato EA et perche il lato GI è incommenſurabile (per la ſettima del decimo di Euclide) al diametro GH ancora il lato FE (ouer CB) (per la decima del decimo di Euclide) ſara incommenſurabile al lato EA |
I would conclude that height AB is 355 steps long. The reason is the following. From my eye (that is, from point E) I take the line EF equidistant to the ground, that is, to the line CB. I move my instrument to the point where the plumb line meets the visual line EA at point H and, similarly, I move the side of the vertical shadow, that is line GI (side of the quadrant), to the point where it meets the same visual line EA at point K. In doing so, the triangle GKH is formed. Since angle GKH is equal (based in the third postulate of the first [book] of Euclid) to angle EFA (for both are right angles) and, similarly, angle KHG is equal (based on the second part of the twenty-ninth [proposition] of the first [book] of Euclid) to angle EAF (based on the second part of the thirty[-second]81 [proposition] of the first [book] of Euclid) angle KGH will be equal to the angle AEF and, therefore, triangle GKH will have the same angles as triangle EAF and will consequently be similar and have proportional sides to one another (based on the fourth [proposition] of the sixth [book] of Euclid). Since triangle GIL will be similar to triangle GKH (based on the second [proposition] of the sixth [book] of Euclid), triangle EAF (based on the twentieth [proposition] of the sixth [book] of Euclid) will be similar to the mentioned triangle GIL and they will have proportional sides to one another. Therefore, the ratio of side EF to side FA is equal to the ratio of side GI to side IL, because side IL is equal to side IG (as both are sides of the quadrant) and, finally, side AF will be equal to side EF. Since the space, that is line CB (based on thirty-fourth [proposition] of the first [book] of Euclid), is equal to the same side EF, it follows (based on the first common sentence [axiom] of the first [book] of Euclid) that part AF of the entire height is equal to the distance, that is, to line CB. Since the residual part FB (of the [entire] height) is equal (based on the thirty-fourth [proposition] of the first [book] of Euclid) to line EC, it follows that (based on the second common sentence [axiom] of the first [book] of Euclid) the sum of the quantity BC to the quantity CE will be equal to the entire height AB, which was the first point to be demonstrated. As the [ratio] of side GI to side GH (diameter of the quadrant) is like [the ratio] of side EF (that is, of side CB) to side EA and since side GI is incommensurable (based on the seventh [proposition] of the tenth [book] of Euclid) to the diameter GH, side FE (that is, side CB) (based on the tenth [proposition] of the tenth [book] of Euclid) will be incommensurable to side EA. |
|
LIBRO TERZO - 24v - cont. |
THIRD BOOK - 24v - cont. |
|
|
et perche il diametro GH è doppio in potentia (per la penultima del I di Euclide) al lato GI ancora il lato EA ſara doppio in potentia al lato EF (ouer CB) quadro adonque il lato EF (ouer CB) (qual ho poſto eſſer paſſa 353) fa 124609 et lo indoppio fa 249218 et di questo indoppiamento piglio la propinqua radice 499
|
Because the square of the diameter GH is double (based on the penultimate [proposition] of the first [book] of Euclid) the side GI, the square of side EA will also be double the side EF (that is, CB) of the quadrangle. Therefore, side EF (that is, side CB) (which I supposed to be 353 steps long) is 124609 and, doubled, makes 249218. Of this result I take the closest square root which is about 499
|
|
LIBRO TERZO - 25r |
THIRD BOOK - 25r |
|
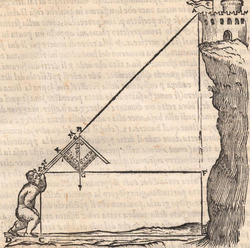 giongeria paßa I con li detti paßa 353 faria paßa 354 e tanto direi che fuſſe la detta altezza AB perche in tal caſo il lato EF è eguale alla partial altezza AF come di ſopra fu dimoſtrado è pero giontoui la quantita FB mi dara total altezza AB che è il propoſito. Propoſitione. IX. Senza mutarme dal luoco doue me ritrouo uoglio comprehendere l’altezza de una coſa apparente, che ſi poſci andare alla baſa, ouer fondamento di quella, et tutto a un tempo uoglio inuestigare la distantia ypothumiſſale, ouer diametrale di tal altezza. |
 I would add one step to the 353 steps, which makes 354 steps and this would be the length of the mentioned height AB, because in such a case, side EF is equal to part AF of the entire height, as has been demonstrated above, and therefore by adding the quantity FB, the total height AB will result in the way it was to be demonstrated. Ninth proposition. Without changing the position of where I am, I would like to know the height of a perceptible object when it is possible to move to its lowest point, that is, to its fundament and, by the same operation, I would like to know the hypotenuse or diametral distance of this height. |
|
LIBRO TERZO - 25r - cont. |
THIRD BOOK - 25r - cont. |
|
|
SIa l’altezza AB della coſa apparente A elleuata et coſtituta ſopra il piano terreo BD talmente che poſcia andare (come nella paßata) alla baſa, ouer fondamento di quella (cioè al ponto B) Dico che uoglio comprehendere la detta altezza AB (ſenza mouermi dal luoco doue me ritrouo[)] et tutto a un tempo |
Let height AB of the perceptible object A be elevated and conceived of over the ground BD so that one can go (as in the previous [proposition]) to its lowest point, that is, to its fundament (that is, to point B). I say that I would like to know the mentioned height AB (without moving from the place where I am[)] and by means of the same operation |
|
LIBRO TERZO - 25v |
THIRD BOOK - 25v |
|
|
uoglio inuestigare la distantia ypothumißale, ouer diametrale di tal altezza. Piglio il mio iſtromento in mano ouer che lo affermo in qualche coſa stabile, et liuello il piano BD et uedo ſe glie perfetto piano (procedendo, come nella ſettima propoſitione fu fatto) et ſe lo trouo perfetto piano, mi appoſto un ponto in la detta coſa apparente qual ſia la uertice A et quella cerco di uedere per li dui forami M, N del mio iſtromento, ſenza mouermi dal luoco doue mi ritrouo, ma torzando, ouer uoltando il detto iſtromento fin a tanto che ueda per li detti dui forami la detta uertice A fatto questo guardo diligentemente donde cade il perpendicolo del detto mio istromento, et ſe quel cadera per caſo, come nella precedente (cioè ſopra la linea de l’ombra media) conchiudero (ſi come fu fatto in la detta precedente) ma ſe quel cadera ſopra il lato de l’ombra retta me dinotara l’altezza AB eſſer maggior del ſpacio che è dalli mei pedi alla baſa, ouer alla radice della detta altezza, cioè al ponto B in tal proportione qual hauera 12 (cioè il lato del quadro) al numero di ponti della ombra retta, doue cade il detto perpendicolo, giontoui la perpendicolare del mio occhio a terra (come ancora nella precedente fu fatto) et questa coſa in la pratica de numeri conchiudero coſi, multiplicaro il numero di paſſa (ouer altra miſura) che è dalli mei pedi al ponto B per 12 et quella multiplicatione partiro per il numero di ponti de l’ombra retta d’onde cade il perpendicolo del mio iſtromento et a quello che uenira al detto partimento, gli agiongero la quantita della perpendicolare del mio occhio a terra, eßempi gratia, poniamo che il perpendicolo del mio iſtromento mi cada ſopra il nono ponto della ombra retta come diſotto appare in figura et pono che dal ponto C [al ponto B] ſia paſſa 25684 et che dal mio occhio a terra, cioé dal ponto E al ponto C ſia paſſa 2 multiplicaro li detti paſſa 256 per 12 (cioe per li dodeci ponti, ouer diuiſioni del lato del quadro, ouer de cadauna ombra) fara 3072 et questo 3072 partiro per 9 (cioe per il numero di ponti de l’ombra retta doue cade il piombino ouer perpendicolo nel mio iſtromento) ne uenira 341
|
I want to investigate the hypotenuse or diametral distance of that height. I take my instrument in the hand or fix it on something stable and then level the ground BD and check whether it is perfectly plane (proceeding according to the method described in the seventh proposition). If I find it to be perfect, I target one point of the mentioned perceptible object, for instance the top of point A, and I try to see it through the two holes M and N of my instrument without me moving but rather by turning the instrument to the right and to the left so that eventually I can see point A through the mentioned holes. Once this is done, I diligently observe where the plumb line of my instrument falls. If it happens to fall like in the previous case (that is, over the middle line of the shadow), I will conclude (in the same way as in the previous [proposition]). But, if it falls on the side of the vertical shadow, this would mean that height AB is longer than the distance between my feet and the lowest point at the fundament of the mentioned height, that is, point B. Such a difference corresponds to the ratio of twelve (that is, the side of the quadrant) to that number of points of the vertical shadow where the mentioned plumb line falls. The [length of] the perpendicular from my eye and the ground has to be added to [the result] of this [ratio] (as has been done in the previous [proposition]). Entering the practice of the numbers, I proceed in the following way. I multiply the number of steps (or of another unit of measurement) by 12, which are between my feet and point B. I then divide this number by the number of points that denote the portion of the vertical shadow where the plumb line of my instrument falls. To the result of this division, I then add the length of the perpendicular from my eye to the ground. For example, suppose that the plumb line of my instrument falls on the the ninth point of the vertical shadow, as shown in the figure below. I then suppose that from point C [to point B]85 there are 25686 steps and that from my eye to the floor there are two steps. I multiply the mentioned 256 steps by 12 (that is, for the 12 points or portions of the side of the quadrant or of each shadow). The result is 3072 and I divide this by 9 (that is, for the number of points of the vertical shadow where the plumb line of my instrument falls). The result is 341
|
|
LIBRO TERZO - 25v - cont. |
THIRD BOOK - 25v - cont. |
|
|
et produco ſimilmente lo lato della ombra retta (cioe la linea partial GI) fin a tanto che concorra ancora lei con la detta linea uiſuale EA in ponto K causando il triangolo GKH et perche l’angolo GKH è eguale (per la terza petitione del I di Euclide) a l’angolo EFA (perche l’uno e l’altro per retto) et ſimilmente l’angolo KHG è eguale (per la ſeconda parte della 2987 del primo di Euclide) a l’angolo EAF onde (per la ſeconda perte della trigeſimaſeconda del I di Euclide) l’angolo KGH uerria a reſtar eguale a l’angolo E[A]F per la qual coſa il triangolo GKH uerria a eſſere equiangolo al triangolo EAF et conſequentemente ſimile, et de lati proportionali (per la quarta del ſeſto di Euclide) et perche il triangolo GIL (per la ſeconda del ſeſto di Euclide) uien a eſſer ſimile al triangolo GKH Adonque il detto triangolo GIL (per la uigeſima del ſeſto di Euclide) uien a eſſer ſimile al medemo triangolo EAF e conſequentemente de lati proportionali, per il che tal proportione ha il lato EF al lato FA qual ha il lato GI al lato IL et perche il lato GI |
Similarly, I change the position of the instrument as much as needed for the side of the vertical shadow (that is, the portion GI [of the line GK]) to meet the mentioned visual line EA at point K. In doing so, I have constructed triangle GKH. Thus, angle GKH is equal (based on the third postulate of the first [book] of Euclid) to angle EFA (for both are right angles) and, similarly, angle KHG is equal (based on the second part of the twenty-ninth88 proposition] of the first [book] of Euclid) to angle EAF. Therefore (based on the second part of the thirty-second [proposition] of the first [book] of Euclid), angle KGH is equal to angle E[A]F.89 For this reason, triangle GHK has the same angles as triangle EAF, and they are consequently similar and have proportional sides to one another (based on the fourth [proposition] of the sixth [book] of Euclid). Since triangle GIL, (based on the second [proposition] of the sixth [book] of Euclid) is similar to triangle GHK, the mentioned triangle GIL (based on the twentieth [proposition] of the sixth [book] of Euclid) is similar to the same triangle EAF and consequently they also have proportional sides to one another. Therefore, the ratio between side EF and side FA is the same as that of side GI to side IL, and the ratio of side GI to |
|
LIBRO TERZO - 26r |
THIRD BOOK - 26r |
|
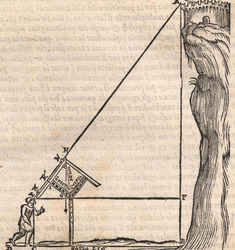 al lato LI è come 9 a 12 (cioè come è li ponti, ouer diuiſioni della parte GI (della ombra retta) a tutto il lato IL del quadrato, il qual lato IL uiene a eſſer tanto quanto le 12 diuiſioni, ouer ponti di tutta la ombra retto) e pero uolendo trouar la quantita de AF (occulta) mediante la notitia de EF (elqual é ſuppoſto eſſer paſſa 256) per la euidentia della uigeſima del ſettimo di Euclide multiplico li detti paſſa 256 per 12 fa 3072 et questo 3072 partiſco per 9 ne uien 341
|
 side LI is like the ratio of nine to twelve (that is, like the points or portions of the part GI) (of the vertical shadow) to the entire side IL of the quadrant, whose side IL is as long as the twelve portions or points of the entire vertical shadow). Thus, while looking for the length AF (unknown) by using the knowledge concerned with EF (which is supposed to be 256 steps) and basing the argument on the twentieth [proposition] of the seventh [book] of Euclid, I multiply the mentioned 256 steps by 12, which makes 3072. I divide this by 9, which makes 341
|
|
LIBRO TERZO - 26r - cont. |
THIRD BOOK - 26r - cont. |
|
|
alla linea EC (la quale è ſuppoſta eſſer paſſa 2) giongo li detti paſſa 2 alli detti paſſa 341
|
to line EC (which is supposed to be two steps long), I add the mentioned two steps to the 341
|
|
LIBRO TERZO - 26v |
THIRD BOOK - 26v |
|
|
paſſa 426
|
426
|
|
LIBRO TERZO - 26v - cont. |
THIRD BOOK - 26v - cont. |
|
|
MA ſe il perpendicolo del mio iſtromento caſcara ſopra il lato della ombra uerſa, all’hora me dinotara che il ſpacio che ſara fra me et la baſa della altezza, con la perpendicolar del mio occhio, ouer con la linea FB eſſer maggiore della altezza della coſa apparente, in tal proportione qual è 12 al numero di ponti della ombra uerſa doue cade il perpendicolo del mio iſtrumento et tal coſa in la pratica de numeri conchiudero in queſto modo multiplicaro il numero di paſſa (ouer altra miſura) che è per retta linea delli mei pedi alla baſa di tal altezza (ouer dal mio occhio al ponto doue che il pian del orizonte ſega quella) per li ponti ouer minuti di l’ombra uerſa (doue cade il piombino del mio istromento) e quella multiplicatione partiro per 12 ouer per 144 et a quello che uenira gli giongero la quantita della perpendicolare del mio occhio a terra (eſſendo in perfetto piano) ouer la quantita, che ſara dal ponto doue ſega quella il pian del orizonte a terra e tanto quanto ſara tal ſuma tanto conchiudero che ſia la detta altezza, eſſempi gratia poniamo che il perpendicolo del mio iſtromento mi cada ſopra il decimo ponto della ombra uerſo, come di ſotto appar in diſegno, et pono che dal ponto C al ponto B ouer dal ponto E, al ponto F ſia paſſa 350 et che dal mio occhio ouer dal ponto F a terra ſia paſſa 2 multiplicaro gli detti paſſa 350 per 10 (cioè per li ponti de l’ombra uerſa doue cada il perpendicolo) fara 3500 et questo 3500 partiro per 12 (cioè per le 12 diuiſioni, ouer ponti de cadauna ombra, ouer del lato dil quadro) ne uenira 291
|
But, if the plumb line of my instrument falls over the horizontal shadow, this then means that the space between me and the lowest point of the height, including the perpendicular from my eye, that is, line FB, is longer than the height of the perceptible object and this according to the ratio of 12 to the number of points of the horizontal shadow, where the plumb line of my instrument falls. In the practice of numbers, I describe this in the following way. I multiply the number of steps (or another unit of measurement) straightly between my feet and the lowest point of the height (or from my eye to the point where the plane of the horizon meets that [line of the height]) by the points or minutes96 of the horizontal shadow (where the plumb line of my instrument falls). I then divide that result by 12 or 14497 and to this result I add the length of the perpendicular from my eye to the ground (if it is perfectly flat) or the quantity between the point, where the perpendicular meets the plane of the horizon and the ground. This sum is then the length of the mentioned height. For example, suppose that the plumb line of my instrument falls over the tenth point of the horizontal shadow, as is shown in the drawing below, and that from point C to point B, or from point E to point F, there are 350 steps, and that from my eye, that is, from point F to the ground, are 2 steps. I multiply the mentioned 350 steps by 10 (that is, by the point on the horizontal shadow where the plumb line falls). This makes 3500 and I divide this by 12 (that is, the 12 portions or points of each shadow or of the side of the quadrant). This results in 291
|
|
LIBRO TERZO - 27r |
THIRD BOOK - 27r |
|
 AB perche dal ochio mio (cioè dal ponto E) duco pur (ſi come nella precedente) la linea EF equidiſtante al piano, ouer linea CB (eßendo perfetto piano il ſpacio terreo CB) ouer la duco ſecondo l’ordine del piano del orizonte, cioè perpendicolarmente ſopra la linea AB in ponto F ancor produco il lato della ombra retta (cioè la linea IO(]) fina a tanto che concorra con il perpendicolo in ponto G cauſando il triangolo ILG il qual triangolo ILG (per le medeme ragioni et argumenti adutti nella demoſtratione della precedente) uien a eßer ſimile al triangolo EAF et perche il triangoletto GOP (per la prima parte della ſeconda del ſeſto di Euclide) uien a eßer ſimile al detto triangolo GIL onde (per la uigeſima del ſesto di Euclide) |
 AB. This happens because (as done previously) I conceive line EF from my eye (that is, from point E) equidistant to the ground, that is, to line CB (as the ground CB is perfectly flat), or I conceive it according to the plane of the horizon, that is, perpendicularly to line AB at point F. I then change the position of the side of the vertical shadow (that is, line IO[)] as much [as] to meet the perpendicular at point G, constructing in this way triangle ILG. This triangle (for the reasons and arguments given in the previous demonstration) is similar to triangle EAF. Since, moreover, the small triangle GOP (based on the first part of the second [proposition] of the sixth [book] of Euclid) is similar to triangle GIL, then (based on the twentieth [proposition] of the sixth [book] of Euclid) |
|
LIBRO TERZO - 27r - cont. |
THIRD BOOK - 27r - cont. |
|
|
il detto triangoletto GOP uien a eßer ſimile al triangolo EAF et perche l’angolo LPQ (del triangolo LPQ) è eguale (per la 15 del I di Euclide) a l’angolo OPG (del triangoletto OPG) et l’angolo LQP del detto triangolo LQP è eguale (per la 3 petitione del I di Euclide) a l’angolo POG (del detto triangoletto POG) perche l’uno e l’altro è retto onde (per la ſeconda parte della trigeſimaſeconda del primo di Euclide) l’altro angolo PLQ (del detto triangolo PLQ) uerria a eßer eguale a l’altro angolo OGP del detto triangoletto OGP per il |
the mentioned small triangle GOP is similar to triangle EAF. Since angle LPQ (of triangle LPQ) is then equal (based on the fifteenth [proposition] of the first [book] of Euclid) to angle OPG (of the small triangle OPG), and angle LQP of the mentioned triangle LQP is equal (based on the third postulate of the first [book] of Euclid) to angle POG (of the mentioned small triangle POG), and because of the fact that both are right angles, therefore (based on the second part of the thirty-second [proposition] of the first [book] of Euclid) the other angle PLQ (of the mentioned triangle PLQ) is equal to the other angle OGP of the mentioned small triangle OGP. Therefore, |
|
LIBRO TERZO - 27v |
THIRD BOOK - 27v |
|
|
che il detto triangolo LPQ uerria a eßer eguale a l’altro angolo OGP del detto triangoletto OGP per il che il detto triangolo LPQ uerria a eßer equiangolo e conſequentemente ſimile, et de lati proportionali al detto triangoletto OPG, et perche il triangolo EFA è ſimilmente ſimile al detto triangoletto OPG Seguita (per la uigeſima del ſeſto di Euclide) che è il detto triangolo LPQ è ſimile al detto triangolo EAF è conſequentemente li lati (continenti, ouer riſguardanti eguali angoli) propotionali (per la quarta del ſeſto di Euclide) per il che tal proportione è dal lato LQ al lato QP qual e dal lato EF al lato AF et perche la proportione del lato LQ al lato QP e ſi come da 12 a 10 (perche il lato LQ uien a eßer tanto quanto e tutto il lato de cadauna ombra, cioè 12 ponti, ouer diuiſioni delle quale diuiſioni, ouer ponti il lato PQ ne e 10) (dal praeſuppoſito) onde per trouare la quantita de AF (incognita) mediante la notitia de EF (el quale e ſuppoſto eßer paßa 350) con la euidentia della uigeſima del ſettimo di Euclide multiplico paßa 350 per 10 (cioè per il lato PQ) fa 3500 e questo 3500 partiſco per 12 (come che ancora in principio fu fatto) (cioè per il lato LQ) mene uien pur 291
|
the mentioned triangle LPQ is equal to the other angle OGP of the mentioned small triangle OGP. Therefore, the mentioned triangle LPQ has the same angles and, consequently, is similar and has proportional sides to those of the mentioned small triangle OPG. Therefore and similarly, triangle EFA is similar to the mentioned small triangle OPG. It follows that (based on the twentieth [proposition] of the sixth [book] of Euclid), the mentioned triangle LPQ is similar to the mentioned triangle EAF and, consequently, the sides (which contain and are turned toward equal angles) are proportional [to each other] (based on the fourth [proposition] of the sixth [book] of Euclid). Therefore, the ratio of side LQ to side QP is the same as of side EF to side AF. Since the ratio of side LQ to side QP is the same as 12 to 10 (because side LQ is as long as the side of each shadow, that is, 12 points or portions, and side PQ is as long as 10 of them), (keeping the suppositions), in order to find the length AF (unknown) by means of the known length EF (which is supposed to be 350 steps), basing the argument on the twentieth [proposition] of the seventh [book] of Euclid, I multiply 350 steps by 10 (that is, side PQ). It makes 3500, which I then divide by 12 (as has been done at the beginning) (that is, by side LQ). The result is 291
|
|
LIBRO TERZO - 27v - cont. |
THIRD BOOK - 27v - cont. |
|
|
fatto questo procedero come fece in principio multiplicaro il lato IL (che è 12) fia il lato EF (che 350) fara 4200 et questo 4200 partiro per li ponti della ombra retta cioè per il lato IG che e 14
|
Once this is done, I proceed as has been done at the beginning. I multiply side IL (which is 12) by side EF (which is 350). It equals 4200 and I divide this by the points of the vertical shadow, that is, by side IG, which is 14
|
|
LIBRO TERZO - 28r |
THIRD BOOK - 28r |
|
|
e paßa circa 455
Propoſitione. X. Voglio artificialmente miſurare l’altezza duna coſa apparente, che non ſi poſcia andare, ne ancor uedere la baſa, ouer fondamento di quella, et tutto a un tempo uoglio inueſtigare la diſtantia ypothumiſſale, ouer diametrale di tal altezza, et ancor a la diſtantia orizontale, cioe quella, che e dal mio occhio al ponto doue il pian del orizonte ſega tal altezza, quantunque tal ponto non ſia apparente, oueramente quella, che e dalli miei piedi rettamente alla baſa, ouer fondamento di tal altezza, quantunque tal baſa, ouer fundamento me ſia occulto. |
and 455
Tenth proposition. I would like to artificially measure the height of a perceptible object, whose lowest point or fundament cannot be seen and to which one cannot go. By means of the same operation, I would like to investigate the hypotenuse or diametral distance of such a height and also the horizontal distance, that is, the distance between my eye and the point where the line of the horizontal distance meets that height, although this point cannot be seen. Similarly, I would like to investigate the length of the line from my feet straight toward the lowest point or fundament of that height, although it cannot be seen. |
|
LIBRO TERZO - 28r - cont. |
THIRD BOOK - 28r - cont. |
|
|
SIa la coſa apparente A l’altezza di la quale (per la terza diffinitione di queſto) è la perpendicolare dutta109 dalla uertice A alla baſa, ouer piano terreo doue eßa altezza ſe ripoßa, il qual piano pongo ſia quello perfetto piano che ſe iſtende (ſe non in atto almen in mente) dal luoco doue me ritrouo equidiſtantemente al pian del orizonte, il qual piano pongo che una parte ne ſia il ſpacio doue ſe iſtende la linea DR et parte della detta altezza, ſia la linea AS il fondamento di la qual altezza uerria a eßer dentro della globoſita terrea T cioè doue concorrariano inſieme le due linee DR et AS eßendo protratte con la mente penetrante la detta globoſita T il qual concorſo pongo che ſia (ſi come nella paßata) il ponto B il qual ponto B non è apparente per cauſa della detta globoſita terrea T hor dico che uoglio artificialmente con lo aſpetto miſurare la detta altezza AB (quantunque non ſi poßa andare ne approßimare alla baſa, ouer fondamento di quella, cioè al ponto B) et tutto a un tempo uoglio ritrouare la distantia ypothumißale, ouer diametrale di tal altezza, et ſimilmente la diſtantia orizontale cioè quella, che è dal mio occhio al punto doue il piano del orizonte ſega tal altezza quantunque tal ponto non ſia apparente per cauſa della globoſita T oueramente quella che è dalli miei piedi per retta linea al fondamento di tal altezza (cioè al ponto B[)] quantunque [t]al ponto B ne ſia occulto per cauſa della detta |
Let there be given the perceptible object A, whose height (based on the third definition of the present work) is the perpendicular line produced110 from top A to the lowest point, that is, to the ground at the point where that height arrives. I suppose that the ground lies perfectly flat (if not in fact, then at least mentally) that extends from the point where I am, equidistant to the plane of the horizon. A part of this plane is supposed to be the space where line DR is drawn. A part of the height is line AS. The lowest part of this height arrives into the spherical ground [designated as] T and if lines DR and AS are mentally extended into the mentioned spherical ground T, they meet, as in the previous [proposition], at point B, which is not visible because of the mentioned spherical ground T. I say that I would like to artificially measure by sight the mentioned height AB (although one cannot get close to the lowest point or fundament of the height, that is, to point B). By the same operation, I would like to find out the hypotenuse or diametral distance of such height and, similarly, the horizontal distance, that is, that distance from my eye to the point where the plane of the horizon meets that height, although this point is not visible because of the spherical ground T. Therefore, I would also find out the distance of the straight line from my feet to the fundament of such a height (that is, to point B[)], although point B is hidden because of the mentioned |
|
LIBRO TERZO - 28v |
THIRD BOOK - 28v |
|
|
globoſita. Piglio il mio iſtromento in mano ouer che lo affermo in qualche coſa ſtabili talmente che ſi poſſa girare da baßo in alto, da poi mi affermo in qualche loco che ſia piu perfetto piano che ſia poßibile e procedo con il detto mio istromento ſi come nella precedente, cioè appoſto un ponto in la detta coſa apparente qual ſia la uertice A et quella cerco di uedere per li dui forami del mio iſtromento fatto questo conſidero ſutilmente ſopra qual lato, ouer ombra cade il perpendicolo del detto istromento, il quale ſel cade (come frequentemente interuiene in tal ſorte di miſurationi) ſopra il lato della ombra uerſa, uedo quanti ponti taglia il detto perpendicolo, et per quel numero de ponti io parto 12 et dapoi ſeruo il numero quotiente eßempi gratia ſe il detto perpendicolo cade ſopra alli 2 ponti, il numero quotiente uien a eßer 6 il qual ſeruo da parte, da poi ſegno il loco nel qual ſon ſtato et poi mi tiro alquanto (rettamente) in drio, ouer che uado alquanto piu inanti del detto loco et un altra uolta in la ſeconda ſtatione cerco da nouo da uedere la detta ſummita, ouer uertice A per li detti forami del detto mio iſtromento, et dapoi guardo diligentemente ſopra quanti ponti della detta ombra uerſa cade il detto perpendicolo, per il qual numero de ponti di nouo parto pur 12 et il numero quotiente che me uiene, lo ſotro, del primo quotiente che fu ſeruato (ſe quel è menore) ouer al contrario ſe quel é maggiore, et ſeruo tal ecceßo, eßempi gratia ſe in la ſeconda ſtatione il perpendicolo cadeße ſopra alli 6 ponti della detta ombra diuido 12 per il detto 6 me uiene per numero quotiente 2 il qual 2 ſottro da l’altro numero quotiente ſeruato che fu 6 lo ecceßo dil qual ſotramento è 4 il qual ecceſſo ſeruo da banda dapoi miſuro il ſpatio, che è fra la prima, et ſeconda ſtatione (con che miſura mi piace) et il numero di quelle miſure diuido per il numero dello ecceßo di ſopra ſeruato, cioè per 4 et a quello che uiene gli agiongo la perpendicolare del mio occhio a terra, et tal ſumma conchiudo che ſia l’altezza della detta coſa apparente. Eſſempi gratia ſel numero delle miſure del detto ſpatio fuße paßa 156 diuido il detto 156 per 4 ne uiene paßa 39 et a questo 39 li agiongo la perpendicolar del mio occhio a terra (qual pongo ſia paßa 2) fa paßa 41 et tanto conchiudo che ſia la detta altezza AB. |
spherical ground. I take my instrument in my hands and fix it onto something stable so that I can turn it upward.111 I then choose a place where the ground is perfectly flat and proceed with the mentioned instrument of mine, as has been said in the previous proposition. Therefore, I target the top of the mentioned perceptible object at point A and try to see that point through the holes of my instrument. Once this is done, I diligently observe over which side or shadow the plumb line of the mentioned instrument falls. If it falls (as often happens in these sort of measurements) over the side of the horizontal shadow, I observe on which point the plumb line falls. I then divide 12 by that number of points, obtaining the quotient number, which I file. For example, if the mentioned line falls over point 2, the quotient number is 6, which I file. I then mark out the place where I was and move (straightly) a little backwards or forwards from the mentioned place. In this second place, I target the mentioned top at point A again through the mentioned holes of the mentioned instrument of mine and, then, I diligently observe over which portion of the mentioned horizontal shadow the plumb line falls. Again, I divide 12 by that number of points and obtain the quotient number. I then subtract the first quotient number from this number, which is filed (if the latter is smaller), or, on the contrary, if the first quotient number is greater, I then subtract from this the second quotient number. Finally, I file this difference. For example, if in the second place the plumb line falls over point 6 of the mentioned shadow, I divide 12 by 6 and obtain 2 as a quotient number. I subtract this from the other filed quotient number, which was 6, and file the difference which is 4. I then measure the space between the first and the second measurement location (using the unit of measurement that I prefer). I then divide this distance by the difference I had filed, that is, 4. To the result of this operation I add the length of the perpendicular from my eye to the ground and conclude that the result of such a sum is the height of the perceptible object. For example, if the number of units of measurement of the mentioned space [between the two measurement locations] is 156 steps, I divide 156 by 4, which makes 39 steps. I add to 39 the length of the perpendicular from my eye to the ground (which I suppose to be 2 steps). The result is 41 steps. I conclude that this is the length of the mentioned height AB. |
|
LIBRO TERZO - 28v - cont. |
THIRD BOOK - 28v - cont. |
|
|
Ma per eßer questa propoſitione alquanto piu difficile delle altre la uoglio reßemplificare un’altra uolta, et uariatamente del ſopra datto eßempio hor poniamo di nouo che nella prima ſtatione (quala pongo ſia doue il ponto C) il perpendicolo del mio iſtromento mi cada ſopra il decimo ponto della ombra uerſa (come di ſotto appar in diſegno) et in la ſeconda ſtatione (quala pongo ſia quella doue il ponto U) mi cada ſopra lo ottauo ponto della detta ombra uerſa (come di ſotto appar in figura) et che dal ponto C al ponto U ſia piedi 285 et che dal occhio mio a terra (cioè dal ponto E al ponto C) ouer dal ponto X al ponto U ſia piedi 4 parto 12 (cioe le 12 diuiſione de cadauna ombra) per 10 cioè per li X ponti che ſega il perpendicolo nella prima ſtatione ne uien 1
|
As this proposition is a bit more difficult than the others, I would like to give another example. This time, it is different than in the example described above. We suppose that at the first measurement location (which is supposed to be at point C) the plumb line of my instrument falls over point 10 of the horizontal shadow (as is shown below in the drawing). At the second measurement location (which is supposed to be at point U), it falls over the eighth point of the mentioned horizontal shadow (as appears below in the drawing). Further, I suppose that the distance from point C to point U is 285 feet and that from my eye to the ground (that is, from point E to point C), or from point X to point U, there are 4 feet. I divide 12 (that is, the twelve portions of each shadow) by 10, that is, for the 10 points over which the plumb line falls at the first measurement location. This makes 1
|
|
LIBRO TERZO - 29r |
THIRD BOOK - 29r |
|
|
fara in ſuma 954 piedi 954 conchiudo che ſia l’altezza della coſa apparente A cioè la linea che è dal ponto A al ponto B (occulto dentro dalla globoſita T[)]. Et per dimoſtrar questo dal occhio dalla 2 ſtatione (cioè dal ponto X) al occhio della I cioè al ponto E duco la linea XE114 et quella produco con la mente fin a tanto che la concorra con la linea AB dentro della globoſita T in ponto F (ſi come nella paſſata) il qual ponto F per eſſer occulto al occhio corporale lo conſideraro con locchio 
|
The result is 954 feet. In conclusion, this is the height of the perceptible object A, that is, the line between point A and point B (which is hidden behind the spherical ground T[)]. And to demonstrate this from the eye of the second measurement location, (that is, from point X) to the eye of the first [measurement station], that is, to point E,115 I conceive line XE116 and prolong it mentally until it meets line AB beyond the spherical ground T at point F (as in the previous [proposition]). As this point F is hidden to the corporeal eye, I consider it by means of the 
|
|
LIBRO TERZO - 29r - cont. |
THIRD BOOK - 29r - cont. |
|
|
mentale, et perche il triangolo AEF (per le ragioni aßignate nella precedente) è ſimile al triangolo LPQ (della prima ſtatione) e tal proportione qual ha la linea ouer lato AF alla linea, ouer lato EF tal ha il lato PQ al lato QL onde (per la decimaterza, et uigeſima prima diffinitione del 7 di Euclide) tante uolte quanto miſurara, ouer intrara il lato PQ in lo lato QL tante uolte miſurara, ouer intrara il lato AF in lo lato EF et perché il lato PQ è ponti 10 et lo lato LQ ne è 12 (dal praeſuppoſito) adonque il lato PQ intrara 1
|
mind’s eye. Since triangle AEF (for the reasons described in the previous [proposition]) is similar to triangle LPQ (of the first measurement location) and line or side AF to line or side EF has the same ratio as side PQ to side QL, therefore (based on the thirteenth and of the twenty-first definition of the seventh [book] of Euclid) side PQ is contained by side QL as many times as side AF by side EF. And, since side PQ is ten points long and side LQ is twelve (as was presupposed), side PQ is contained 1
|
|
LIBRO TERZO - 29v |
THIRD BOOK - 29v |
|
|
triangolo LPQ della detta ſeconda statione, et che tante uolte quanto intra il lato PQ (che è ponti 8) in lo lato LQ (che è ponti 12) tanto intrara il lato AF in lo lato XF et perché il lato PQ (cioè ponti 8) intra 1
|
triangle LPQ of the mentioned second measurement location. Thus, side PQ (which is eight points long) is contained by side LQ (which is twelve points) as many times as side AF is contained by side XF. Since side PQ (which is eight points) is contained 1
|
|
LIBRO TERZO - 29v - cont. |
THIRD BOOK - 29v - cont. |
|
|
vero è, che per altre uie piu facile io potria trouar le dette diſtantie ypothumißale et ſimilmente tutte le altre commenſurationi, le qual uie ſariano molto al propoſito per quelli che non ſano radicare ne pratica de numeri, ma per eſſer difficile a dicchiarirle in ſcrittura, le laßo. Biſogna notare per queſte ſorte de operationi doue ſi procede con due poſitioni che la perpendicolare del mio occhio a terra nella piu propinqua ſtatione ſarà alquanto menore di quella della ſtatione piu lontana et maßime eßendo il detto iſtromento fiſſo in qualche coſa ſtabile et quantunque tal differentia ſia poca coſa, nondimeno alle uolte puo cauſar non poco errore, et per tanto eſſorto a fondarſe nella perpendicolare, che ſarà da quel pironcino doue ſta attacato il piombino per inſino a terra ſi in l’una come in l’altra ſtatione, il qual pironcino uien a eſſer il centro di tal istromento, et congignando il detto iſtromento girabile in qualche coſa che ſtia in piedi, come ſono li lucernari, el ſi debbe congegnare da l’altra banda di tal iſtromento vn pirone fermo a dirimpeto del pironcino del piombino, talmente che tal iſtromento uenghi a girare ſopra il ſuo centro, perche girando ſopra altro ponto, ſempre ui correrà alquanto di errore nella concluſione. Hor per ritornar al nostro propoſito, ſe per ſorte io fuße pur tanto appreſſo della detta altezza, che il perpendicolo mi caſcaße ſopra la ombra retta, vederò medeſimamente quanti ponti gli harà il detto perpendicolo di detta ombra retta, et procederò al contrario del precedente modo, cioè io partirò li detti ponti tagliati dal detto perpendicolo, per 12 del qual partimento neceßariamente |
It should also be added that I could find out the mentioned hypotenuses as well as all other measurements by means of other methods, which are easier, especially for those who are not able to calculate the square root and are not practiced with numbers. However, as these methods are difficult to describe by means of writing, I will not discuss them.122 One also has to note that, in these sort of operations when two positions [for the measurement] are involved, the perpendicular from my eye to the ground at the closest position is a little shorter than the one at the position further away, especially when the instrument is fixed on something stable. Although such a difference is small, it can sometimes cause a large mistake. Therefore, I exhort to drive [the instrument] at both places, along the perpendicular which starts at the small pivot where the plumb line is fixed, down to the ground. In this way, that small pivot becomes the center of the instrument. If the instrument is conceived as turning around on something that stands, for instance, on poles to hang lamps, the instrument should be designed to have a pivot on the other side of the point where the small pivot for the plumb line is. In this way, the instrument rotates around its center. Otherwise, if it turns around another point, an error will always occur in the conclusions. Now, to go back to our purpose, if it happens that I am so close to the mentioned height that the plumb line falls on the vertical shadow, I again observe the point over which the plumb line of the mentioned instrument falls. But, I then proceed in the opposite way as the previous method. Namely, I divide the number of points indicated by the plumb line by 12 and, from this division, a |
|
LIBRO TERZO - 30r |
THIRD BOOK - 30r |
|
|
ne venirà ſempre un rotto; el qual rotto ſeruarò da banda, et dapò ſegnarò il loco nel qual ſarò ſtato, et dapoi me tirarò alquanto rettamente in drio, ouer che andarò alquanto piu inanti del detto luoco, (come fu fatto nell’altra ſopradetta operatione) et vn’altra volta in la ſeconda ſtatione cercarò di nouo di veder la detta ſommità, ouer vertice A per li detti forammi del detto iſtromento, et dapoi guardarò diligentemente ſopra quanti ponti della detta ombra retta caderà il detto perpendicolo, li quali ponti di nouo li partirò per 12 del qual partimento neceßariamente me ne venirà vn rotto, et queſto tal rotto lo cauarò da quell’altro primo che fu ſeruato da banda, (eßendo però menor di quello,) oueramente cauarò quel primo da queſto ſecondo, eßendo maggiore, et queſto reſtante ſeruarò da banda, dapoi miſurarò il ſpacio, che è fra la prima, et ſeconda ſtatione, con che miſura me parerà, et il numero di queſte tal miſure partirò per quel mio reſtante (ſeruato da banda) et a quello auenimento gli aggiongo la perpendicolare, che ſarà dal centro del mio iſtromento à terra (cioè da quel ponto doue ſta attacato il perpendicolo) et tal ſumma conchiuderò che ſia l’altezza della detta coſa apparente. Eßempi gratia, ſe nella prima poſitione, ouer ſtatione, il perpendicolo, ouer piombino mi caſcaße ſopra lo terzo ponto della ombra retta, io parteria li detti 3 ponti per 12 (lato del quadro) et me ne ueneria
|
fraction of a number necessarily results. I file this fraction and then I mark the place where I am. Then, following a straight line, I move backwards or forwards (as has been done in the above-mentioned operation). Then, I try to see the mentioned top at point A through the holes of the mentioned instrument again. Further, I diligently observe over which point of the vertical shadow the plumb line follows and I divide this number by 12. From this division, a fraction necessarily results. I subtract this last fraction from the first, which was filed (if the second is smaller than the first), or I subtract the first from the second, if the second is greater. I then file the result of the subtraction. Then, I measure the space that is between the first and second measurement location, according to the unit of measurement that I prefer. Then, I divide this number by that remaining (filed away) and to this result I add the length of the perpendicular from the center of my instrument to the ground (that is, from that point where the plumb line is fixed). I conclude that this result is the height of the mentioned perceptible object. For example, if at the first measurement location the plumb line falls over the third point of the vertical shadow, I divide the mentioned 3 points by 12 (side of the quadrant) and the result is
|
|
LIBRO TERZO - 30r - cont. |
THIRD BOOK - 30r - cont. |
|
|
In queſte ſorte de comenſurationi doue biſogna operare con due poſitioni, ouer in dui colpi, egliè neceßario a eßer molto diligente in queſto, che quella coſa doue ſarà conzignato il noſtro iſtromento girabile ſtia talmente perpendicolare nel ſecondo luoco come che ſtaſeua preciſamente nel primo, perche non ſtaſendo coſi preciſe non poco errore cauſarebbe, et queſto ſi può conoſcere con el piombino medeſimo del noſtro iſtromento, ouer con un’altro aßettato in quella tal coſa. |
In this sort of measurement method, where one has to operate at two positions, that is, at two times, it is very necessary to be diligent in making sure that at the two different measurement locations the instrument stands exactly equally perpendicular. If the instrument did not stand precisely in the same way, this would cause a relevant error. This can be controlled by means of the plumb line of the instrument itself, or by means of another plumb line fixed to another object. |
|
LIBRO TERZO - 30v |
THIRD BOOK - 30v |
|
|
Propoſitione. XI. Mi uoglio fabricare un’altro iſtromento che mi ſerua comodamente a inuiſtigare con l’aſpetto le diſtanze orizontale et ancora le ypothumiſſale delle coſe apparente. PIglio una lamina di rame, ouer di ottone ben piana groſſa circa a una coſta di cortello, et di quella ne cauo un quadro piu giuſto che ſia poßibile (per gli modi dati nella quinta propoſitione di questo) et nel detto quadrato li ne diſegno un’altro alquanto menor del primo, talmente che li quatro lati di queſto ſecondo quadro ſiano egualmente diſtanti delli lati del primo et queſto faccio per laſſarui quel poco interuallo per mettere li numeri delle diuiſioni de cadauno lato del detto quadro, ouer iſtromento, et in queſto ſecondo quadro gli ne diſegno uno altro terzo quadro tanto menor del ſecondo, che li lati di questo terzo ſiano egualmente diſtanti delli lati del ſecondo circa a quatro coste di cortello et piu, è manco ſecondo la grandezza ouer picolezza del primo quadrato, et questo ſecondo interuallo lo laſſo per mettere le diuiſioni di lati del detto iſtromento, et fatto queſto diuido cadauno lato di queſti tre quadrati in due parti eguali, et dal centro di tal quadro a ciaſcaduna di quelle diuiſioni tiro una linea retta et per eſſer meglio inteſo ſia il primo quadro ABCD con li altri dui quadrati inſcritti come nella ſequente figura appar, et le linee che uengono dal centro K del detto quadro, alla mitta di ciaſcun lato ſiano le due linee EF et GH le quale due linee uengano a diuidere ciaſcadun lato di questi tre quadrati in due parti eguali, hor dico che questo iſtromento non uoria eßer men di una ſpanna per fazza, ouer per lato. Il che eßendo ogni mita del lato del 2 quadrato uol eßer diuiſo in 12 parti le quali 12 parti ſe chiamano ponti, talche cadaun lato del detto 3 quadrato ueria a eßer diuiſo in 24 ponti ponti, cioè 12 in una mita et 12 nell’altra mitta, et tutte queſte 12 et 12 ponti cominciano a numerar dalla mitta di ciaſcun lato andando uerſo langolo ſia da una banda come da l’altra, et per eßer piu pronto a numerar li detti ponti in quel interuallo che fra li lati del primo et ſecondo quadro ui ſi gli mette il numero a ciaſcadun ponto cioè 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 et 12 |
Eleventh proposition. I would like to manufacture another instrument that I can comfortably use to investigate by sight the horizontal distances and the hypotenuses of perceptible objects. I take a foil of copper, or brass, which is flat and about as thick as the width of the blade of a knife. From it, I produce a square as correct as possible (following the procedures described in the fifth proposition of the present work). Within this square, I draw another square a little bit smaller than the first and in such a way that the four sides of the second square are equally distant from the sides of the first squares. The space between the two squares has to be large enough to write the numbers of the portions of each side of the mentioned square or instrument in it. I then draw a third square within the second, whose sides are equally distant from the sides of the second. The third square should be equidistant to the second square and its sides at a distance from the second, which is about four times the blade of a knife, more or less according to the largeness or smallness of the first square. This second space is left for the marks of the portions of the sides of the mentioned instrument. Once this is done, I divide each side of those three squares into two equal parts. Then, I draw a straight line to each of those divisions from the center of the quadrant. In order to be more comprehensible, let ABCD be the first square with the other two squares inscribed, as is shown in the following figure. The lines that start at the center K of the mentioned quadrant and that go to the middle points of each side are the two lines EF and GH. These two lines divide each side of these three squares into two equal parts. Now I say that this instrument should not be smaller than a span at each side. Then, each half of the sides of the second square is divided into twelve equal parts and these are called points, so that each of the sides of the third square is also divided into twenty-four points, that is, twelve on one half and twelve on the other half. All these twelve and twelve points are enumerated, starting from the middle of each side and then toward the angle on both sides. In order to improve the use of the points, all of these portions are enumerated in the space between the first and second square by assigning a number to each portion, that is, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. |
|
LIBRO TERZO - 30v - cont. |
THIRD BOOK - 30v - cont. |
|
|
et il primo ponto in l’una e l’altra mita principia nella mita dil lato (cioè doue che le due linee GH et EF ſegano li lati del detto ſecondo quadrato) et il 12 ponto di luna et l’altra mita uien a fenire nelli quatro angoli dil detto 3 quadrato et acio che tai 12 et 12 diuiſioni per ciaſcun lato ſiano piu euidente ſe diuide tutto quel ſpacio che è fra li lati del ſecondo et terzo quadrato, et con lineette che venghino dal centro K del quadro a cadauna di quelle 12 et 12 diuiſioni gia fatti in ciaſcun lato del ſecondo quadrato. Et oltra di queſto ciaſcaduno di questi 12 et 12 ponti de ciaſcun lato ſi debe diuidere ancora in altre 12 parti eguali, le quali ſe chiamano minuti, et farli euidenti con lineette tirate dal centro K come fu detto di ponti, et fatto queſto a cadauno lato del detto ſecondo quadrato uera a eſſer diuiſo in 288 minuti, cioè 144 in ciaſcaduna mitta del lato, et 144 ne l’altra mitta. Ma perche queſta coſi minuta diuiſione non ſi puo mandar a eßecutione in un quadrato piccolo, nondimeno per eſſer meglio inteſo te pongo in figura ſotto |
The first point, on both halves, is at the middle of the side (that is, where the two lines GH and EF meet the sides of the second square). And the twelfth point of both halves is at the angles of the mentioned third square. In order to make each of these twelve and twelve portions on each side more visible, the space between the sides of the second and the third square are divided by small lines drawn from center K of the quadrant toward each of those twelve and twelve divisions already marked on each side of the second square. Moreover, each of these twelve and twelve points of each side are divided again into a further twelve equal parts, which are called minutes. These have to be made visible by means of small lines from center K, in the same way as has been said for the points. Once this is done, each side of the mentioned second square is divided into 288 minutes, 144 on each half of the sides. Because such a division by minute cannot be executed on a small square, in order to make this clearer, I show you |
|
LIBRO TERZO - 31r |
THIRD BOOK - 31r |
|
|
lo ſcritto quadretto del quale ogni mita del lato del ſecondo, è diuiſo ſolamente in ſie parti, ma per accordarſe con quello che ſe ha da dire, ſupponeremo che ciaſcaduno di queſti uaia per doi ponti. [I]l numero di detti ponti per la ſtretezza del ſpacio non ui ſe ſono potuti accomodar, ma baſta a ſaper che doue finiſſe il primo ponto dal E uerſo B ſe gli pone I et doue finiße il ſecondo ui ſi gli mette 2 et coſi procedendo per fin in 12 el qual 12 ponto uien a terminare nel angolo B del ſecondo quadrato il medeſimo ſi debbe fare nell’altra mitta uerſo A cioè nel fin del primo ponto dal E uerſo A m[e]tterui I et in fin del ſecondo 2 et coſi andar procedendo per fin in 12 il qual 12 uien a fenire nel angolo A del ſecondo quadrato, et tutto queſto che ſe é detto del lato AB del detto ſecondo quadrato ſi debbe intendere et fare in li altri tre lati AC, CD et DB del detto ſecondo quadrato, cioé principiar a numerar alli ponti di mezzo, cioè G, F, H del detto ſecondo quadrato et fenir nelli angoli A, B, C, D et biſogna aduertire, come diſopra fu detto, che li detti numeri di ponti uogliono eßer posti in quelli interualli che ſono ſra li lati del primo quadro, et quelli del ſecondo. Oltra di queſto biſogna far una dioptra, ouer traſguardo il qual traſguardo uolendo far de un pezzo ſolo el ſi debbe tuor quella lamina di ottone, ouer di rame piana, et tirar in quella (con una rega iuſtisſima) una linea retta longa quanto che è il diametro del quadrato del iſtromento qual in queſto caſo ſaria quanto che è dal A al D ouer dal B al C et queſta tal linea ſuppono che ſia la retta LM et questa ſia diuiſa in due parti eguali in ponto N et ad angoli retti con un’altra retta linea, a quella eguale la qual pongo ſia la OP et ſopra il ponto N faccio un circoletto picolo, et un altro ſimile et eguale a quello ne ſia deſcritto in cadauna iſtremita di queſte due linee, cioè ſopra li ponti L, M, O, P et di queſta figura cauarne fuora quattro brazza in croce perfetta, ma talmente che il corpo de cadauno di queſti quattro brazza ſia al contrario del uoſtro contrapoſito come di ſotto ſi uede in figura. |
a small square drawn in the figure below, where each half of the sides of the second square is divided into only six parts. In order to associate what I am going to say with this figure, we suppose that each of these portions corresponds to two points. Because of the smallness of the space [in the drawing below], the number of the mentioned points could not be written, but it is sufficient to know that where the first portion from E toward B ends, there I suppose 1. Where the second portion ends, I suppose 2, and so on until 12, which is placed at angle B of the second square. The same has to be done in the other half of the square toward A. Therefore, I suppose 1 at the end of the first portion from E toward A, 2 at the end of the second, and so on until 12, which is at angle A of the second square. All that has been said and done in reference to side AB has to be conceived and done in reference to the other three sides AC, CD and DB of the mentioned second square. This means starting the enumeration at the middle points, that is, G, F and H of the mentioned second square and moving toward angles A, B, C and D. As has been said above, one has to note that those numbers of the points have to be written in the space between the sides of the first and of the second square. Besides this, one has to construct a dioptra or sight. This sight should be made of a unique piece and obtained from a foil of brass or very flat copper. (By using a very perfect ruler) one draws on that foil a straight line as long as the diameter of the square of the instrument, which, in this case, is as long as the distance between point A to point D, or from point B to point C. I suppose that this line is the straight line LM. I divide this line into two equal parts at point N. At right angles [I draw] another straight line, equal to the first, and I suppose this to be line OP. Then, I draw a small circle at point N and at each end of these two lines I draw four equal circles, that is, at the ends of the lines or points L, M, O and P. Using this figure, I obtain [from the foil] four arms perfectly crossing each other but in a way that the body of each of these arms extends on the back of the lines, as is shown in the figure. |
|
LIBRO TERZO - 31r - cont. |
THIRD BOOK - 31r - cont. |
|
 Ma biſogna uſar diligentia, che quelli lati che paſſano per il centro N ſiano rettamente tagliati, li quali lati uengono a eſſer le prime due linee tirate nel principio, |
 One has to work diligently and consider that those sides that go through center N have to be straightly and correctly cut and that these sides correspond to the first two lines that were drawn, |
|
LIBRO TERZO - 31v |
THIRD BOOK - 31v |
|
|
cioè la linea LM et OP. Fatto queſto biſogna aſſettare nel centro di cadauno di quelli quatro cerchij L, M, O, P una ponta alla ſimilitudine della ponta Q oueramente una laminetta con uno buſetino alla ſimilitudine della laminetta R che oppoſitamente ſe incontrino per traſguardar le coſe. Et doppo questo biſogna con un pironcino impironare il centro N della dioptra, ouer traſguardo ſopra il centro K del noſtro iſtromento talmente che la detta dioptra ſia girabile ſopra il detto centro K onde eſſendo ben fatta, et aſſettata li effetti ſuoi ſaranno di tal ſorte che ogni uolta che ſia girata talmente che la linea LM della dioptra caſchi preciſamente ſopra la linea EF del iſtromento neceſſariamente l’altra linea OP della detta dioptra caſcara praeciſamente ſopra la linea GH del detto iſtromento, et quando che coſi ſtia tal dioptra, la ſe ripoſſara rettamente ſopra dil noſtro istromento, ſimilmente tal dioptra ſe diria ripoſſarſe rettamente ſopra del detto iſtromento quando che la linea LM di tal dioptra caſcaſſe praeciſamente ſopra la linea GH del iſtromento, il che eſſendo l’altra linea PO della detta dioptra, ueneria a caſcar ſopra la linea EF del detto iſtromento, et queſto tal iſtromento per operarlo, biſogna da l’altra banda congegnarui di poterlo accomodare in cima d’un baſtone alto almen tre piedi il qual baſtone per operarlo alla foreſta biſogna che da l’altro capo habbia un ferro appontito di poterlo piantar in terra, ma per operarlo in lochi doue non ſi poteſſe piantare in terra ui ſe potria far a tal baſtone un pie alla ſimilitudine di quelli lucernali che ſi coſtumano per ficar le lucerne. Et uolendo che tal istromento ne ſerua comodamente non ſolamente per inuiſtigare una diſtantia orizontale, ma ancora le ypothumiſſale, ouer diametrale, cioè di ſotto inſuſo diametralmente, ouer di ſuſo in giuſo pur ypothumiſſalmente. Biſogna congegnar tal istromento in la cima di quel baſtone, come ſon dui poli talmente che leuandolo dalla parte dananti, la parte di drio ſi uenghi ad abbaßar in uerſo terra, et al contrario elleuandolo dalla parte di drio, la parte denanti ſe abbaßi uerſo terra il che facendo ſe potra traſguardar non ſolamente per il piano del orizonte, ma de ſotto in ſuſo, et di ſuſo in giuſo. Oltra di queſto biſogna notare, che tal quadrato ſe potria deſignar in carta groſſa, e ben liſſa, et dapoi incolarlo ſopra d’un quadretto di tauola di legno groſſa almen un buon dedo, et ſecca, et dapoi farui una dioptra di legno ſecondo l’ordine datto nel 7 queſito del 5 libro delli noſtri queſiti per fare la dioptra del boſſolo per tor in diſſegno, uero è che ſe potria far il detto iſtromento de legno, e carta come è detto, et poi far la detta dioptra de ottone, et ſara piu honoreuole et durabile. |
which are the lines LM and OP. Once this is done, a small head, similar to the head Q or a small foil with a small hole, similar to the foil R, has to be fixed at the center of each of those circles L, M, O and P. They have to be appropriately set to target the things by sight. After this has been done, one has to fix a pivot at the center N of the dioptra, that is, of the sight, over center K of our instrument and in such a way that the mentioned dioptra can be turned around the mentioned center K. Thus, if the instrument is well manufactured and assembled, it shows that each time it is turned so that line LM of the dioptra falls precisely over line EF of the instrument, then the other line OP of the mentioned dioptra necessarily falls over line GH of the mentioned instrument. If the dioptra is rightly placed over the instrument, it is said that the dioptra is rightly placed over the instrument when line LM of the dioptra falls precisely over line GH of the instrument. If this happens, the other line PO of the mentioned dioptra falls over line EF of the mentioned instrument. In order to use this instrument, it has to be fixed on the other side at the top of a stick at least three feet high. If such a stick has to be used in the forest, it must have a point of iron on the other side so as to be able to drive it into the ground. If, however, it has been used in places where it is not possible to drive it into the ground, it should be provided with a foot similar to those used for the poles on which lamps hang. If the instrument has to be used not only to find out the horizontal distance, but also the hypotenuse or diametral distance, that is, upwards toward the diameter or downward also toward the diameter or hypotenuse, one has to design the instrument on the upper part of that stick like two poles. Using these, if one raises the front [of the instrument], then the rear lowers itself and, on the contrary, if one raises the rear, then the front lowers itself toward the ground. If this is done, the instrument can be used not only to target horizontal distances, but also upwards and downwards. Besides this, one has to note that the square could be drawn onto a thick and smooth piece of paper, which is then glued on to a small square of wood, at least as thick as a thumb, and dry. Then a dioptra could be prepared according to the instructions given in the seventh quesito of the fifth book of our Quesiti,123 in order to use the dioptra of the compass as a surveying instrument. It is moreover true that one could make the mentioned dioptra out of wood and paper, as I said, but then one would make the mentioned díoptra out of brass, which is more honorable and durable. |
|
LIBRO TERZO - 31v - cont. |
THIRD BOOK - 31v - cont. |
|
|
Propoſitione. XII. Eglie posſibile a inuistigare, et conſcere la diſtantia de una coſa apparente, oſia orizontale, ouer ypothumiſſale o uogliam dire diametrale. SIa prima il ponto A ſituato nel piano del horizonte dico che eglie poßibile a conſiderare, ouer conoſcere quanto ſia da me diſtante, et per inuistigar questo, |
Twelfth proposition. How to know the distance, that is, the horizontal distance and the hypotenuse or diametral distance of a perceptible object. First, let point A be located on the plane of the horizon. I say that it is possible to consider, or to ascertain how distant it is from me. To know this, |
|
LIBRO TERZO - 32r |
THIRD BOOK - 32r |
|
|
piglio il mio fabricato iſtromento, et lo pianto rettamente cioè perpendicolarmente in terra, et acontio la dioptra, ouer traſguardo talmente che ſtia rettamente ſopra del detto iſtromento (cioè ſecondo che fu diffinito nella precedente) dapoi torzo et retorzo tanto detto iſtromento che per due di quelle ponte, ouer buſi della detta dioptra io ueda il detto ponto A et uisto che io habbia (poniamo per le due ponte, ouer buſi B, C della retta dioptra come nella ſequente figura appare) mi formo un’altra linea perpendicolare (cioè a ſquara) ſopra la linea BCA et per formarla ſenza muouere il detto iſtromento, ne manco la retta dioptra, ouer traſguardo per le altre due ponte, ouer buſi D, E direttamente, et fazzo piantar per un gran tramito di lontano due bacchette rettamente in terra, l’una diſtante almen 4 ouer 5 paſſa l’una da l’altra, ma talmente che ambe due caſchino ſotto del detto mio traſguardo, cioè ſotto la retta linea DEF le qual bachette in queſto caſo pongo che l’una ſia in ponto G et l’altra nel detto ponto F et queſte due bachette le fazzo piantare accio mi conſeruino et dimoſtrino la detta linea DEFG fatto queſto cauo el detto mio iſtromento (ſenza mouere la dioptra della ſua rettitudine) et me diſcosto per quanti paſſa me parera dal detto luoco primo, et questo diſcoſtamento lo poſſo far da qual banda mi pare, cioè, ouer uerſo le due bachette gia piantate, ouer dalla parte conuerſa, ma per al preſente me uoglio diſcoſtar andando uerſo le due bachette, cioè uerſo li dui ponti G, F et tal diſcoſtamento pongo che ſia paßa 15 nel qual loco pianto de nouo il detto mio iſtromento, |
I take my manufactured instrument and set it righty and perpendicularly into the ground. I assemble the dioptra or sight so that it will be placed at a right angle over the instrument (that is, as has been defined in the previous [proposition]). Then, I turn the mentioned instrument back and forth as much as needed to see that mentioned point A through two of those points or holes of the mentioned dioptra. Once I have targeted it (for instance through the two points or holes B and C of the straight dioptra, as appears in the figure below), I conceive of another line, perpendicular (according to the square) over line BCA. In order to realize this without moving the instrument and the dioptra, I watch through the other two points or holes D and E, and along that straight line I let two rods far away from me drive perfectly straightly into the ground with a distance between them other of at least four or five steps. Both of them have to be on the line that goes through D and E, that is, on line DEF.124 The two rods are supposed to be placed at point G and the other at point F. I let these rods drive into the ground so that they mark and show me the mentioned line DEFG. Once this is done, I take my instrument out of the ground (without moving the dioptra from its perpendicular position) and I move from that location as many steps as I would like to. It is also possible to move toward both sides, that is, either toward the two driven rods or toward the opposite side. Now, I would like to change positions and move toward the two rods, that is, toward the two points G and F. I then suppose to move fifteen steps away and in that place I drive my instrument into the ground again. |
|
LIBRO TERZO - 32r - cont. |
THIRD BOOK - 32r - cont. |
|
|
ma talmente che ſia nella medeſima linea, che ne dinotara le dette due bachette il che facilmente ſe conoſcera traſguardando et incontrando le due ponte, ouer buſi D, E della retta dioptra con le dette due bachette, ſi come fu fatto nel primo loco, et fatto questo eglie coſa chiara che ſtante la detta dioptra retta ſopra dil detto istromento (in questo ſecondo luogo) et guardando per le due ponte, ouer buſi B, C non ſi potra uedere il ponto A anci ſara forza (uolendolo uedere per 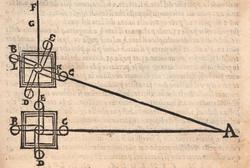
|
This I do in such a way that it is placed on the same line marked by the two rods. This can easily be checked by targeting the two rods through the two points or holes D and E of the straight dioptra, as has been done at the first measurement location. Once this is done, it is clear that if the mentioned dioptra is placed right over the mentioned instrument (in this second measurement location), by watching through the two points or holes B and C, one cannot see point A. But to target it (that is, to see point A 
|
|
LIBRO TERZO - 32v |
THIRD BOOK - 32v |
|
|
le dette due ponte, ouer buſi il detto ponto A) a obliquare, ouer torzere la detta dioptra (ſenza mouer liſtromento) con la ponta, ouer buſo C uerſo il detto A come che nella figura del 2 luoco appare, et fatto questo guardo diligentemente quanto ſe ſia diſcoſtata la linea BC della dioptra dalla ſua rettitudine cioè dal ponto H et questo lo conoſcero per uigor di ponti, et minuti gia deſcritti nel lato del 2 quadro cioè quanti ne reſtaranno discoperti fra H et I hor poniamo che dal H a I ſiano 4 ponti, cioè de quelli che ciaſcaduna mitta del 2 quadrato [(]ne è 12) diro per la regola uolgarmente detta del 3 ſe 4 ponti mene da 12 per la mitta del lato che me dara quelli 15 paßa che hauemo ſuppoſto che ſia dal loco doue ſe piantò prima lo iſtromento al luoco doue ſe pianto alla 2 uolta, onde multiplicaro quelli 15 paßa per 12 fara 180 et questo partiro per 4 mene uenira 45 et paßa 45 conchiudero che ſia dal luoco doue che prima ſe piantò liſtrumento al ponto A et coſi ſe per ſorte ogni ponto fuße diuiſo in 12 minuti et che per ſorte dal ponto H al ponto I ſuße, poniamo caſo minuti 8 io direi ſe minuti 8 mi da minuti 144 (cioè la mitta del lato del quadro) che mi dara paßa 15 onde multiplicaria li detti paſſa 15 fia li detti minuti 144 faria 2160 et questo parteria per li 8 minuti ne ueniria paßa 270 et paſſa 270 conchiederia che fuſſe dal detto luoco doue che ſe piantò prima il detto noſtro iſtromento per fin al detto ponto A et coſi procedaria nelle altre ſimile. hor per dimoſtrar la cauſa di tal nostra operatione per abreuiar il dire nel centro del iſtromento della prima poſitione intenderemo un K et nel centro di quello della 2 poſitione intenderemo un N et arguiremo in questo modo, perche la linea LH è equidiſtante alla linea KA langolo HNI del triangoletto HNI ſara eguale (per la 29 del I di Euclide) al angolo A del triangolo NAK (per eſſer alterni) et ſimilmente l’angolo K del triangolo NAK è eguale al angolo H del triangoletto NHI per eſſer l’uno, e l’altro retto onde per la 32 del 1 di Euclide li detti dui triangoli KAN et HNI ſaranno equiangoli, et (conſequentemente per la 4 del 6 di Euclide) ſaranno de lati proportionali onde la proporzione del lato HI al lato NH ſara, come quella del lato KN al lato KA |
through the mentioned two points or holes) it will be necessary to turn the mentioned dioptra (without moving the instrument) with point, or hole C toward the mentioned point A, as it appears in the second place in the figure. Once this is done, I diligently observe how far line BC has moved away from the right line, that is, from point H. I will ascertain this difference by means of the points and minutes that are written on the side of the second square. I therefore observe how many [points] there are between points H and I. Now, supposing that between H and I there are four points, that is, [(]four of the twelve) of which each half of the second square is constituted. Based on the rule, popularly known as the rule of three, we can suppose that if we have four points of those twelve of the half of the side and those fifteen steps that we suppose to be the distance between the place where the instrument was driven in the ground the first time and the second time, then, when I multiply those 15 steps by 12, which makes 180, and divide this sum by 4, the result is 45. Then, I conclude that the distance from the place where the instrument was driven first at point A is 45 steps. In the same way, if each point were divided into 12 minutes and if there were 8 minutes between point H and point I, I would say that we have eight minutes, then 144 minutes (which is half of the side of the square) and then fifteen steps. Thus, I multiply the mentioned 15 steps by the mentioned 144 minutes, which makes 2160. I divide this by those 8 minutes and the result is 270 steps. I conclude that the distance between the first point where the mentioned instrument was driven into the ground and point A is 270 steps long. I proceed in the same way in other similar cases. Now, to demonstrate the cause of our operation and in order to keep this explanation short, we say that the center of the instrument at the first place is called K, while the center of the same in the second position is N. We proceed as follows. Since line LH is equidistant from line KA, angle HNI of the small triangle HNI is equal (based on the twenty-ninth [proposition] of the first [book] of Euclid) to angle A of triangle NAK (as they are alternate).125 Moreover, since similarly angle K of triangle NAK is equal to angle H of the small triangle NHI, as they are both right angles, because of the thirty-second [proposition] of the first [book] of Euclid, the mentioned two triangles KAN and HNI will have the same angles and (consequently, based on the fourth [proposition] of the sixth [book] of Euclid) all the sides are proportional to each other. Hence, side HI to side NH will have the same ratio as side KN to side KA. |
|
LIBRO TERZO - 32v - cont. |
THIRD BOOK - 32v - cont. |
|
|
et perche nel principio fu ſuppoſto che il lato HI fuße punti 4 et il lato HN uien a eſſer ponti 12 (per eſſer egual alla mitta del lato del quadro) et il lato NK fu ſuppoſto eßer paſſa 15 onde per ritrouar il lato KA cognito per la euidentia della 16 del 6 di Euclide multiplico il lato KN (cioè paſſa 15) per il lato HN [(]cioè per ponti 12) fa 180 et questo parto per il lato HI cioè per li 4 ponti che mi ſcopre la dioptra (dal preſupoſito) mene uiene 45 et paßa 45 diremo che ſia il lato KA come che in principo fu determinato et coſi ſe procedaria quando chel ponto A fuſſe piu in alto ouer piu baſſo del orizonte alzando, ouer abaßando la parte dauanti del iſtromento ſtante pero sempre il bastone doue ſara fitto perpendicolare a lorizonte ſi in monte come in piano et ſimilmente le due bacchette che ſe piantaranno ſi debbono sempre perpendicolarmente et tai bacchette uogliono eſſer rettißime, et la tramutatione che ſe fara dal I al 2 loco con listromento, biſogna che ſia egualmente diſtante dal piano del orizonte. Oltra di questo biſogna conſiderar diligentemente, e minutamente, li ponti et minuti et parte di minuto che laſſara ſcoperti la dioptra, cioè la quantita de HI perche ogni picolo errore che ſi faceſſe in li detti minuti cauſariano errore molto euidente nella concluſione perche tai ponti, ouer minuti uengono a eſſer partitore, et ogni minimo errore che ſi faccia nel partitore non poco fa uariar lo auenimento. IN VINEGIA. M. D. LVIII. |
Moreover, since it was supposed at the beginning that the side HI is four points long, and side HN is twelve points long (as it is equal to half of the side of the square), and side NK was supposed to be fifteen steps long, in order to find out the unknown side KA, based on the sixteenth [proposition] of the sixth [book] of Euclid, I multiply side KN (that is, fifteen steps) by side HN [(]that is, by twelve points). This makes 180 and I divide this by side HI, that is, by the four points shown by the dioptra (as it was supposed). This makes 45 and I say that the length of side KA is 45 steps long, as was determined above. The procedure then remains the same, also in the case of point A being higher or lower than the horizon, as the front of the instrument can be raised or lowered. But the stick always has to be driven perpendicularly to the horizon, on the mountains as well as on flat ground. Similarly, the two rods always have to be driven perpendicularly to the ground and such rods have to be very straight and, when the instrument is moved from the first to the second place, it then has to be driven again at the same distance from the plane of the horizon. Besides this, it has to be said that the points, minutes and parts of minutes shown by the dioptra, when turned and in space HI, have to be observed very diligently and precisely. In fact, each small error in the observation of those minutes would cause a very evident error in the conclusion, because those points and minutes are divisors and each small error made concerning the divisor can cause the quotient to vary enormously. IN VENICE. M. D. LVIII. |
Footnotes
1537 edition: “Invention newly found by Nicolo Tartaglia from Brescia, very useful for all speculative mathematical bombardiers and for others, entitled Nova scientia, divided into five books.”
“Naturals” means natural philosophers. In the 1537 edition, the following words are inserted here: “according to the authority of Galen, Avicenna and many other very excellent physicists.”
“Fires” means fireworks.
Tartaglia is referring to Castel Vecchio in Verona.
“Schioppo” can also be translated with “blunderbuss.”
In the 1537 edition, “Highly Respected Lord” is inserted here.
Santa Lucia is an old town close to Verona.
In the 1537 edition, “Distinguished Lord” is inserted here.
1537 edition: “ratiocinare” instead of “invistigare.”
In the 1537 edition, “videlicet” is inserted here.
According to Medieval Aristotelian terminology, “accidents” means “qualities” here.
In the 1537 edition, “Very Serene Lord” is inserted here.
Here, “oblique” means that the cannon points to a point lower than the place where the artillery is located.
In the 1537 edition, “Very Benevolent Lord” is inserted here.
1537 edition: “Archimedane.”
In the 1537 edition, “Very Excellent Duke” is inserted here.
In the 1537 edition, “Very Liberal Duke” is inserted here.
1537 edition: “ratiocinar” instead of “saper.”
In the 1537 edition, “Very Prudent Lord” is inserted here.
In the 1537 edition, “Very Open Minded Lord” is inserted here.
In the 1537 edition, “Very Respected Lord” is inserted here.
The last sentence was added in the 1550 edition.
1537 edition: “battere” instead of “tirare.”
Here, to “know the quantities” means to calculate transits and ranges.
The words “depths” and “widths” were added in the 1550 edition.
Johann Stöffler.
Orontio Fineo (Oronce Fine).
1537 edition: “utile” instead of “necessarie.”
Following the 1537 edition, the last two sentences read: “Besides this, Very Calm Lord, out of curiosity I began to read the Pandects, Avicenna and many other very excellent physicists in order to understand the origin and nature of different kinds of gum, salt, oil, distilled water and also of simple minerals and other non mineral [products] produced by nature and manufactured by art. I also found some of their peculiar characteristics pertinent to the art of fires. Moreover, I investigated which of the mentioned materials are suitable to be joined together and which are not able to burn together.”
In the 1537 edition, “Very Magnanimous Duke" is inserted here.
The words “human beings” were added in the 1550 edition.
In the 1537 edition “Oh Very Excellent Duke” is inserted here.
Tartaglia refers here to the Ottomans.
In the 1537 edition, “Very Magnanimous Lord” is inserted here.
In the 1537 edition, “Most Illustrious Lord” is inserted here.
Fen is an old denomination for the sections of Avicenna’s work Liber canonis and of other works translated into Latin from Arabic.
The bodies are considered to be in the places where they naturally belong.
Gravity is considered here as a quality shared by the bodies.
The suggestion concerning the wedge-shaped object was inserted in the 1550 edition.
1537 edition: “astrologice” instead of “astronomatice.”
A common sentence is an axiom.
In the 1537 and 1550 editions, the first common sentence was followed by a short commentary: “One has to note that the mentioned height has to be conceived in respect of [the position] of the resistant.” A similar sentence follows the third common sentence.
Il testo originale riporta erroneamente la lettera “C” al posto della lettera “A.”
The original text mistakenly reads “C” instead of “A.”
The body that falls from point A.
From this point until the end of the proposition, the text was added in the second edition of 1550.
La stampa del 1558 riporta erroneamente la lettera “D” al posto della lettera “A.”
The original text of the 1558 print run mistakenly reads “D” instead of “A.” This mistake was introduced in the 1558 print run of the 1550 second edition.
La stampa del 1558 riporta erroneamente “AB” al posto di “AH.”
“C” is missing in the 1558 print run.
The 1558 print run mistakenly reads “AB.”
The 1558 edition mistakenly repeats “Third definition.”
La stampa del 1558 riporta erroneamente “dentro” al posto di “centro.”
The 1558 print run reads “dentro.” A comparison of the 1537 and 1550 editions shows that the term “centro” was meant.
“Equidistant” refers here to the distance between all points that compose the lines of the transits toward the center of the world. As these lines are parallel, all the corresponding points are equidistant to each other. The fact that in reality those transits are not parallel because they meet at the center of the world is discussed by Tartaglia in the following.
La stampa del 1558 riporta erroneamente “CE” al posto di “C.”
The 1558 print run mistakenly reads “CE.”
La stampa del 1558 riporta erroneamente “SH” al posto di “FH.”
The 1558 print run mistakenly reads “SH.”
La stampa del 1558 riporta erroneamente “AEDG” al posto di “AEFG.”
The 1558 print run mistakenly reads “AEDG.”
“Different manners” means here at different elevations.
“Equal” means here at the middle point.
The commentator Tartaglia refers to is Johannes Campanus.
“Portion of a circle” means here sector of a circle.
To understand Tartaglia’s argument, a distinction has to be made between his two different statements. In the first case, he specifies that it is the angle “composed on the arc,” meaning the angle composed by the chord and the line that joins the point where the chord ends above the circumference and the point where the arc ends. According to the second statement, Tartaglia means the angle composed by the chord, where it ends, and the part of circumference, that is, the curved line. The meaning of the second statement becomes clear only at the end of the argument.
For a better understanding of Tartaglia’s argument, it should be considered that the violent motion is the composition of the straight and curved parts.
“Distance” should be understood as range.
During the Renaissance and in the framework of algebra, Italian mathematicians used the term “cosa,” which means “thing,” to express what nowadays would be defined as the “unknown” or simply “x.” Given this peculiarity, the term will not be translated but left as it is and set in italics.
La stampa del 1558 riporta erroneamente “290” al posto di “200.”
A “censo” is the product of a cosa by itself, or the square.
The 1558 print run mistakenly reads 290.
The decimals are eliminated by rounding up or down.
The correct reading is found in the 1537 edition only.
“Variety of shots” means here elevations of shots.
These spaces are the areas of the triangles with point E as vertex.
The paragraph entitled “Correction of the author” was added in the 1550 edition.
In the 1537 edition, “in the hands” was inserted here.
In the 1537 edition, “in the hands” was inserted here.
The method is described in the seventh proposition of the third book.
The 1537 and 1550 editions read correctly.
La stampa del 1558 riporta erroneamente “
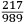 ” al posto di “
” al posto di “
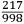 .”
.”
The 1537 and 1550 editions and the 1558 print run mistakenly read
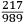 . This was proved by means of the method described by Tartaglia in the second book of the second volume of the General trattato di numeri et misure to calculate the square root.
. This was proved by means of the method described by Tartaglia in the second book of the second volume of the General trattato di numeri et misure to calculate the square root.
La stampa del 1558 riporta erroneamente “236” al posto di “256.”
The 1537 and 1550 editions read correctly.
The 1558 print run mistakenly reads “236.”
La stampa del 1558 riporta erroneamente “26” al posto di “29.”
The 1558 print run mistakenly reads “26.”
The 1558 print run mistakenly reads “EF.”
La stampa del 1558 riporta erroneamente “
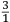 ” al posto di “
” al posto di “
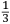 .”
.”
The 1558 print run mistakenly reads “
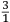 .”
.”
La stampa del 1558 riporta erroneamente “
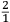 ” al posto di “
” al posto di “
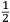 .”
.”
The 1558 print run mistakenly reads “
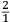 .”
.”
The last two sentences were added in the 1550 edition.
La stampa del 1558 riporta erroneamente “
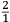 ” al posto di “
” al posto di “
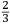 .”
.”
The specification “or minutes” was added in the 1550 edition.
The specification “144” minutes was added in the 1550 edition.
The number “2” is specified in the 1537 and 1550 editions.
The 1558 print run reads “
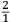 .” The 1550 edition is not readable at this point. The 1537 edition correctly reads “
.” The 1550 edition is not readable at this point. The 1537 edition correctly reads “
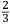 .”
.”
La stampa del 1558 riporta erroneamente “ILG al lato L” al posto di “IG al lato IL.”
The 1558 print run mistakenly reads “ILG to side L.”
La stampa del 1558 riporta erroneamente “75059
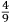 ” al posto di “85069
” al posto di “85069
 .”
.”
La stampa del 1558 riporta erroneamente “270569
 ” al posto di “207569
” al posto di “207569
 .”
.”
La stampa del 1558 riporta erroneamente “455
 ” al posto di “455
” al posto di “455
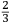 .”
.”
The 1558 print run mistakenly reads “75059
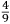 .”
.”
The 1558 print run mistakenly reads “270569
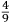 .”
.”
The 1558 print run mistakenly reads “455
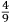 .”
.”
The last sentence was added in the 1550 edition.
La stampa del 1558 riporta erroneamente “tutta” al posto di “dutta.”
The 1558 print run mistakenly reads “tutta” instead of “dutta.”
The part of the sentence from “fix” to “upward” was added in the 1550 edition.
La stampa del 1558 riporta erroneamente “10” al posto di “X.”
The 1558 edition mistakenly reads “10” instead of “X.”
La stampa del 1558 riporta erroneamente “YE” al posto di “XE.”
In the 1537 edition, the last sentence from “And to demonstrate” to “ point E” reads in the following way: “Because from my eye at the second [measurement] location (that is, from point X) to the eye of the first [measurement location] (that is, to point E).”
The 1558 print run mistakenly reads “YE” instead of “XE.”
The 1558 print run mistakenly reads “
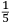 ” instead of “1
” instead of “1
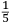 .”
.”
La stampa del 1558 riporta erroneamente “LQ” al posto di “PQ.”
La stampa del 1558 riporta erroneamente “LQ” al posto di “PQ.”
The 1537 edition reads “LQ” instead of “PQ.”
The 1537 edition reads “LQ” instead of “PQ.”
The 1537 first edition of Tartaglia’s Nova scientia concludes here in the following way: “It is true that I could find alternative and easier methods to find the diametral distances, which would be very appropriate for those who are not able to calculate the square roots and who do not even know what the square root is. However, as these subjects are difficult to explain in written form, I decided to show them actively that is, by viva voce. Similarly, I do not show [how to calculate] the horizontal distances, or how to measure the widths and depths of the perceptible things, because these subjects are not very relevant for the bombardiers. I intend to speak about these particular things with more ease another time.”
The first location for measurements is illustrated in the lower part of the figure.
The angles are on the two sides of the same transversal line that meets two parallel lines.

 onde la detta retta AH uenneria a eſſer circa a quatro uolte tanto è vn ſettimo della retta AE che è il propoſito.
onde la detta retta AH uenneria a eſſer circa a quatro uolte tanto è vn ſettimo della retta AE che è il propoſito.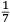 . Therefore, the mentioned line AH is about four times and one seventh the straight line AE, which was to be demonstrated.
. Therefore, the mentioned line AH is about four times and one seventh the straight line AE, which was to be demonstrated.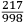
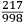 (uel circa) diro che ſara la diſtantia ypothumiſſale, ouer diametrale EA che è il ſecondo propoſito. Ma ſe per caſo il piano terreo BD non fuſſe perfetto piano (come la maggior parte delle uolte accade[)] pigliaro il ponto doue ſegara il pian del orizonte tal altezza AB liuelando col mio iſtromento ſi come in la propoſitione precedente fu fatto, qual pongo ſia il ponto F poi cerco con induſtria di miſurare la linea EF ouer una equidiſtante a quella, et a quella quantita non gli agiongo piu la quantita EC ma ben in luoco di quella gli agiongo la quantita FB et tanto quanto ſara tal ſuma, tanto diro che ſia la detta altezza AB. eßempi gratia ſe la linea EF fuſſe (come diſopra fu ſuppoſto) paßa 353 et che la linea FB fuſſe paſſa 3
(uel circa) diro che ſara la diſtantia ypothumiſſale, ouer diametrale EA che è il ſecondo propoſito. Ma ſe per caſo il piano terreo BD non fuſſe perfetto piano (come la maggior parte delle uolte accade[)] pigliaro il ponto doue ſegara il pian del orizonte tal altezza AB liuelando col mio iſtromento ſi come in la propoſitione precedente fu fatto, qual pongo ſia il ponto F poi cerco con induſtria di miſurare la linea EF ouer una equidiſtante a quella, et a quella quantita non gli agiongo piu la quantita EC ma ben in luoco di quella gli agiongo la quantita FB et tanto quanto ſara tal ſuma, tanto diro che ſia la detta altezza AB. eßempi gratia ſe la linea EF fuſſe (come diſopra fu ſuppoſto) paßa 353 et che la linea FB fuſſe paſſa 3
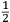 io giongero li detti paſſa 3
io giongero li detti paſſa 3
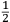 con li paßa 353 fara paſſa 356
con li paßa 353 fara paſſa 356
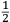 e paßa 356
e paßa 356
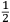 diro che ſia la detta altezza AB et coſi procedaria quando che la linea FB fuße menor della linea EC cioe, ſe la fuße ſolun paßa I
diro che ſia la detta altezza AB et coſi procedaria quando che la linea FB fuße menor della linea EC cioe, ſe la fuße ſolun paßa I and I will say that the hypotenuse or diametral distance EA is 499
and I will say that the hypotenuse or diametral distance EA is 499
 steps (more or less),
steps (more or less), steps long, I will add the mentioned 3
steps long, I will add the mentioned 3
 steps together with the 353 steps, which makes 356
steps together with the 353 steps, which makes 356
 , therefore the mentioned height AB is 356
, therefore the mentioned height AB is 356
 steps long. And I would proceed as follows if line FB were shorter than line EC. If it were only one step long,
steps long. And I would proceed as follows if line FB were shorter than line EC. If it were only one step long, et a questo 341
et a questo 341
 gli agiongero paſſa 2 (cioe la quantita de EC) fara 343
gli agiongero paſſa 2 (cioe la quantita de EC) fara 343
 e paſſa 343
e paſſa 343
 conchiudero che ſia la detta altezza AB. Perche dal occhio mio (cioè dal ponto E) duco (ſi come nella precedente) la linea EF equidiſtante al piano, ouer linea CB et produco il perpendicolo del mio iſtromento fin a tanto, che quel concorra con la linea uiſuale EA in ponto H
conchiudero che ſia la detta altezza AB. Perche dal occhio mio (cioè dal ponto E) duco (ſi come nella precedente) la linea EF equidiſtante al piano, ouer linea CB et produco il perpendicolo del mio iſtromento fin a tanto, che quel concorra con la linea uiſuale EA in ponto H and to this result I add the two steps (that is, the quantity EC). The result is 343
and to this result I add the two steps (that is, the quantity EC). The result is 343
 and this is the length of height AB. I conceive of line EF (as in the previous [proposition]) from my eye (that is, from point E) equidistant to the ground, that is, to line CD, and I change the position of my instrument so that its plumb line meets the visual line EA at point H.
and this is the length of height AB. I conceive of line EF (as in the previous [proposition]) from my eye (that is, from point E) equidistant to the ground, that is, to line CD, and I change the position of my instrument so that its plumb line meets the visual line EA at point H.
 faranno paſſa 343
faranno paſſa 343
 et tanto conchiudero che ſia tutta la altezza AB ſi come ancora in principio fu fatto, che il primo propoſito. Et perche ſi come é il lato GI al lato, ouer ypothumiſſa GH coſi é il lato EF al lato, ouer ypothumiſſa EA et perche il lato GI al lato, ouer ypothumiſſa GH (per la penultima del primo di Euclide) come 9 alla radice quadrata de 225 che è 15 onde per trouar lo lato, ouer ypothumißa EA (occulta) (per la euidentia della uigeſima del ſettimo di Euclide) multiplico 15 fia la quantita di EF (la quale e ſuppoſta eſſer paßa 256) fa 3840 et questo 3840 partiſco per 9 ne uiene
et tanto conchiudero che ſia tutta la altezza AB ſi come ancora in principio fu fatto, che il primo propoſito. Et perche ſi come é il lato GI al lato, ouer ypothumiſſa GH coſi é il lato EF al lato, ouer ypothumiſſa EA et perche il lato GI al lato, ouer ypothumiſſa GH (per la penultima del primo di Euclide) come 9 alla radice quadrata de 225 che è 15 onde per trouar lo lato, ouer ypothumißa EA (occulta) (per la euidentia della uigeſima del ſettimo di Euclide) multiplico 15 fia la quantita di EF (la quale e ſuppoſta eſſer paßa 256) fa 3840 et questo 3840 partiſco per 9 ne uiene steps, which is 343
steps, which is 343
 , and I conclude that this is the length of the entire height AB, as it has been done in the beginning and which was to be shown first. Since the ratio of side GI to side or hypotenuse GH is like the ratio of side EF to side or hypotenuse EA and since the ratio of side GI to side or hypotenuse GH (based on the penultimate [proposition] of the first [book] of Euclid) is likewise to the ratio between 9 and the square root of 225, which is 15, hence, in order to find [the length of] the side or hypotenuse EA (unknown) (based on the twentieth [proposition] of the seventh [book] of Euclid), I multiply 15 by the length of EF (which is supposed to be 256 steps), which makes 3840. I then divide 3840 by 9 and this results in
, and I conclude that this is the length of the entire height AB, as it has been done in the beginning and which was to be shown first. Since the ratio of side GI to side or hypotenuse GH is like the ratio of side EF to side or hypotenuse EA and since the ratio of side GI to side or hypotenuse GH (based on the penultimate [proposition] of the first [book] of Euclid) is likewise to the ratio between 9 and the square root of 225, which is 15, hence, in order to find [the length of] the side or hypotenuse EA (unknown) (based on the twentieth [proposition] of the seventh [book] of Euclid), I multiply 15 by the length of EF (which is supposed to be 256 steps), which makes 3840. I then divide 3840 by 9 and this results in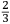 diro che ſia la diſtantia ypothumifſale, ouer diametrale AE che è il ſecondo propoſito. Ancora per la penultima del I di Euclide Io potea trouar la detta ypothumiſſa EA multiplicando il lato EF in ſe che ſaria 65536 ancora il lato FA in ſe che faria 116508
diro che ſia la diſtantia ypothumifſale, ouer diametrale AE che è il ſecondo propoſito. Ancora per la penultima del I di Euclide Io potea trouar la detta ypothumiſſa EA multiplicando il lato EF in ſe che ſaria 65536 ancora il lato FA in ſe che faria 116508
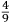 et queſti dui quadrati gionti inſieme fariano 182044
et queſti dui quadrati gionti inſieme fariano 182044
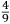 et di queſta ſumma pigliandone la radice quadrata la qual ſaria pur 426
et di queſta ſumma pigliandone la radice quadrata la qual ſaria pur 426
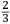 ſi come per l’altra uia fu trouato e tanto diria che fuſſe la detta distantia ypothumiſſale EA che ſaria pur il medemo ſecondo propoſito. Ma ſe per caſo il piano terreo BD non fuſſe perfetto piano (come la maggior parte delle uolte accade) procedero ſi come nella precedente liuelando, et miſurando con induſtria la linea EF et poi procedero ſi, come diſopra è ſtato fatto eccetto che in luoco della linea EC gli agiongero la quantita FB o ſia piu, ouer meno de paſſa 2 et coſi conchiudero il propoſito. Et ſe per caſo il perpendicolo del mio ſtromento non mi caſcaſſe ſopra integral ponto, ouer diuiſione, eſſempi grati[a] ſel me caſcaſſe ſopra al nono ponto è mezzo del decimo, cioè a ponti 9
ſi come per l’altra uia fu trouato e tanto diria che fuſſe la detta distantia ypothumiſſale EA che ſaria pur il medemo ſecondo propoſito. Ma ſe per caſo il piano terreo BD non fuſſe perfetto piano (come la maggior parte delle uolte accade) procedero ſi come nella precedente liuelando, et miſurando con induſtria la linea EF et poi procedero ſi, come diſopra è ſtato fatto eccetto che in luoco della linea EC gli agiongero la quantita FB o ſia piu, ouer meno de paſſa 2 et coſi conchiudero il propoſito. Et ſe per caſo il perpendicolo del mio ſtromento non mi caſcaſſe ſopra integral ponto, ouer diuiſione, eſſempi grati[a] ſel me caſcaſſe ſopra al nono ponto è mezzo del decimo, cioè a ponti 9
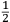
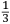 procederia pur ſi come diſopra è ſtato fatto multiplicando la detta diſtantia cioé li paſſa 256 per 12 et tal multiplicatione partiria per 9
procederia pur ſi come diſopra è ſtato fatto multiplicando la detta diſtantia cioé li paſſa 256 per 12 et tal multiplicatione partiria per 9
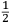 ouer 9
ouer 9
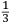 et a quello che ueniße gli agiongerei la perpendicolar del mio occhio, ouer la quantita FB et tanto quanto fuſſe tal ſuma, tanto conchiuderei che fuſſe la altezza AB et coſi mi gouernarei in ogni altro rotto de ponto, ouer diuiſione, che è il propoſito E pero per fuggir li rotti laudo a douer diuider ciaſcaduno di 12 et 12 ponti in altre 12 parti (come fu detto nella coſtrution dello detto iſtrumento) li quali ſi chiamano minuti per il che cadauna ombra ueria a eſſer diuiſa in 144 minuti.
et a quello che ueniße gli agiongerei la perpendicolar del mio occhio, ouer la quantita FB et tanto quanto fuſſe tal ſuma, tanto conchiuderei che fuſſe la altezza AB et coſi mi gouernarei in ogni altro rotto de ponto, ouer diuiſione, che è il propoſito E pero per fuggir li rotti laudo a douer diuider ciaſcaduno di 12 et 12 ponti in altre 12 parti (come fu detto nella coſtrution dello detto iſtrumento) li quali ſi chiamano minuti per il che cadauna ombra ueria a eſſer diuiſa in 144 minuti.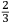 steps. I say that this is the hypotenuse or diametral distance AE which was to be shown secondly. Differently and by means of the penultimate [proposition] of the first [book] of Euclid, I could have found the mentioned hypotenuse EA by multiplying side EF with itself, which makes 65536, and then side FA with itself, which makes 116508
steps. I say that this is the hypotenuse or diametral distance AE which was to be shown secondly. Differently and by means of the penultimate [proposition] of the first [book] of Euclid, I could have found the mentioned hypotenuse EA by multiplying side EF with itself, which makes 65536, and then side FA with itself, which makes 116508
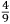 , and these two squares added together make 182044
, and these two squares added together make 182044
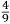 . I then calculate the square root of this sum, which is also 426
. I then calculate the square root of this sum, which is also 426
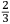 , as has been calculated by means of the other method. This then would be the length of the hypotenuse EA which is again what was to be shown secondly. If, however, the ground BD is not perfectly flat (as happens most of the time) I proceed, as said previously, by leveling and precisely measuring line EF. I then proceed as described above, with the exception of adding length FB instead of line EC, that is, either more or less than two steps, and so I have shown what was to be shown. If it happens that the plumb line of my instrument does not fall precisely over a point or portion but falls, for example, between point 9 and point 10, that is, at point 9
, as has been calculated by means of the other method. This then would be the length of the hypotenuse EA which is again what was to be shown secondly. If, however, the ground BD is not perfectly flat (as happens most of the time) I proceed, as said previously, by leveling and precisely measuring line EF. I then proceed as described above, with the exception of adding length FB instead of line EC, that is, either more or less than two steps, and so I have shown what was to be shown. If it happens that the plumb line of my instrument does not fall precisely over a point or portion but falls, for example, between point 9 and point 10, that is, at point 9
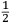
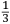 , I proceed as shown above by multiplying the mentioned distance of 256 steps by 12 and would divide such a result by 9
, I proceed as shown above by multiplying the mentioned distance of 256 steps by 12 and would divide such a result by 9
 or 9
or 9
 and add to this result the length of the perpendicular from my eye, that is, length FB. And I say that this result is the length of the entire height AB. I would proceed in the same way each time one has to deal with fractions of points, or of portions, which was to be shown. To avoid such fractions, however, I consider dividing each of the twelve, and twelve points into a further twelve parts (as said in the description of the construction of such instrument) to be a good method. These parts are called minutes and each shadow would be divided into 144 minutes.
and add to this result the length of the perpendicular from my eye, that is, length FB. And I say that this result is the length of the entire height AB. I would proceed in the same way each time one has to deal with fractions of points, or of portions, which was to be shown. To avoid such fractions, however, I consider dividing each of the twelve, and twelve points into a further twelve parts (as said in the description of the construction of such instrument) to be a good method. These parts are called minutes and each shadow would be divided into 144 minutes. et a questo 291
et a questo 291
 gli giongero 2 (cioè li [2] paßa che hauemo ſuppoſto che ſia dal ponto E al ponto C ouer dal ponto F al ponto B) fara 293
gli giongero 2 (cioè li [2] paßa che hauemo ſuppoſto che ſia dal ponto E al ponto C ouer dal ponto F al ponto B) fara 293
 et paſſa 293
et paſſa 293
 and to it I add 2 (those are the [two]
and to it I add 2 (those are the [two]
 (come prima) et tanto diro, che ſia la partial altezza AF et perche il reſiduo FB è ſuppoſto eßer paßa 2 agiongo li detti paßa 2 alla quantita AF (cioè a 291
(come prima) et tanto diro, che ſia la partial altezza AF et perche il reſiduo FB è ſuppoſto eßer paßa 2 agiongo li detti paßa 2 alla quantita AF (cioè a 291
 [)] fa 293
[)] fa 293
 et paßa 293
et paßa 293
 conchiudero che ſia la total altezza AB ſi come in principio fu fatto che è pur il primo propoſito. Io poßo ancora per vn’altro modo trouar la detta altezza AB fondandomi ſopra il triangolo LIG elqual ſo che e ſimile al triangolo AEF et tal proportione qual ha il lato IG al lato IL
conchiudero che ſia la total altezza AB ſi come in principio fu fatto che è pur il primo propoſito. Io poßo ancora per vn’altro modo trouar la detta altezza AB fondandomi ſopra il triangolo LIG elqual ſo che e ſimile al triangolo AEF et tal proportione qual ha il lato IG al lato IL e ponti 24
e ponti 24
 diro che ſia la ombra retta IG
diro che ſia la ombra retta IG (as before) and I say that this is the length of the portion AF [of the height AB]. Since the remaining part FB is supposed to be 2 steps long, I add these two steps to the quantity AF (that is, to 291
(as before) and I say that this is the length of the portion AF [of the height AB]. Since the remaining part FB is supposed to be 2 steps long, I add these two steps to the quantity AF (that is, to 291
 [)]. The result is 293
[)]. The result is 293
 , which is the number of steps of the entire height AB, as achieved at the beginning and was the first thing to be demonstrated. I can also ascertain the height of AB by other means. The reasoning [of this other method] is based on the fact that triangle LIG is similar to triangle AEF and the ratio between side IG to side IL,
, which is the number of steps of the entire height AB, as achieved at the beginning and was the first thing to be demonstrated. I can also ascertain the height of AB by other means. The reasoning [of this other method] is based on the fact that triangle LIG is similar to triangle AEF and the ratio between side IG to side IL, and I will say that 24
and I will say that 24
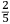 points is [the length of] the vertical shadow IG.
points is [the length of] the vertical shadow IG.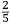 ne uenira 291
ne uenira 291
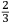 per il lato AF (ſi come per l’altro modo) dapoi gli agiongero la quantita FB cioè paßa 2 fara pur paſſa 293
per il lato AF (ſi come per l’altro modo) dapoi gli agiongero la quantita FB cioè paßa 2 fara pur paſſa 293
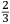 che è pur il primo propoſito. Et perche ſi come è il lato LQ al lato (ouer ypothumißa[)] LP ſi e il lato EF al lato (ouer ypothumißa) EA et perche il lato LQ al lato ouer ypothumißa LP (per la penultima del I di Euclide) e come 12 alla radice quadrata di 244 onde per trouar lo lato, ouer ypothumißa EA (occulta) (per la euidentia della 20 del 7 di Euclide) multiplico lo lato EF (cioè paßa 350) fia la radice quadrata di 244 fara radice quadrata 29890000 loqual partiſco per 12 ne uien radice quadrata 207569
che è pur il primo propoſito. Et perche ſi come è il lato LQ al lato (ouer ypothumißa[)] LP ſi e il lato EF al lato (ouer ypothumißa) EA et perche il lato LQ al lato ouer ypothumißa LP (per la penultima del I di Euclide) e come 12 alla radice quadrata di 244 onde per trouar lo lato, ouer ypothumißa EA (occulta) (per la euidentia della 20 del 7 di Euclide) multiplico lo lato EF (cioè paßa 350) fia la radice quadrata di 244 fara radice quadrata 29890000 loqual partiſco per 12 ne uien radice quadrata 207569
 la qual ſara circa 455
la qual ſara circa 455
 è paßa 455
è paßa 455
 uel circa diro che ſia la distantia ypothumißale, ouer diametrale AE che è il ſecondo propoſito. Ancora per la penultima del I di Euclide. Io potea trouar la detta ypothumißa EA multiplicando il lato EF in ſe, che faria 122500 ſimilmente il lato FA in ſe che faria 85069
uel circa diro che ſia la distantia ypothumißale, ouer diametrale AE che è il ſecondo propoſito. Ancora per la penultima del I di Euclide. Io potea trouar la detta ypothumißa EA multiplicando il lato EF in ſe, che faria 122500 ſimilmente il lato FA in ſe che faria 85069
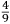
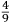 (la qual ſaria circa) 455
(la qual ſaria circa) 455
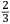 .
.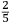 . The result is 291
. The result is 291
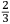 , which is side AF (as it resulted by means of the other method). I then add to this the length FB, that is, two steps. The result is 293
, which is side AF (as it resulted by means of the other method). I then add to this the length FB, that is, two steps. The result is 293
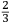 steps, which was to be shown first. Since side LQ to side (or hypotenuse[)] LP has the same ratio as side EF to side (or hypotenuse) EA and since side LQ to side or hypotenuse LP (based on the penultimate [proposition] of the first [book] of Euclid) has the same ratio of twelve to the square root of 244, hence, to find side or hypotenuse EA (unknown) (based on the twentieth [proposition] of the seventh [book] of Euclid) I multiply side EF (that is, 350 steps) by the square root of 244, which is the square root of 29890000. I divide this by 12, which makes a square root of 207569
steps, which was to be shown first. Since side LQ to side (or hypotenuse[)] LP has the same ratio as side EF to side (or hypotenuse) EA and since side LQ to side or hypotenuse LP (based on the penultimate [proposition] of the first [book] of Euclid) has the same ratio of twelve to the square root of 244, hence, to find side or hypotenuse EA (unknown) (based on the twentieth [proposition] of the seventh [book] of Euclid) I multiply side EF (that is, 350 steps) by the square root of 244, which is the square root of 29890000. I divide this by 12, which makes a square root of 207569
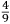 , which is ca. 455
, which is ca. 455
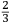 . This is the number of steps of the hypotenuse or diametral distance AE, which was to be shown secondly. Another method based on the penultimate [proposition] of the first [book] of Euclid: I can find the mentioned hypotenuse EA by multiplying side EF by itself, which makes 122500 and, similarly, side FA by itself, which makes 85069
. This is the number of steps of the hypotenuse or diametral distance AE, which was to be shown secondly. Another method based on the penultimate [proposition] of the first [book] of Euclid: I can find the mentioned hypotenuse EA by multiplying side EF by itself, which makes 122500 and, similarly, side FA by itself, which makes 85069
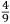 .
.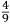
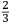
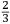 diria che fuße la detta ypothumißa EA ſi come che ancora per l’altra uia fu determinato che è il propoſito, et ſe per caſo il piano terreo non fuße piano, ouer che il perpendicolo caſcaße ſopra alcuna parte di ponto, ouer de diuiſione procederia ſi come nella precedente, et per conoſcer meglio le dette parti ouer frattioni diuidero cadaun ponto, ouer diuiſione, ſi de l’ombra retta come della uerſa (come diſopra fu ancor detto) in altre dodeci parti, et cadauna di quelle chiamaremo minuto: la qual diuiſione mi ſara molto accomoda per trouar le dette altezze, et ancora le diſtantie ypothumiſſale et orizontale ſenza mouermi dal luoco doue me ritrouo.
diria che fuße la detta ypothumißa EA ſi come che ancora per l’altra uia fu determinato che è il propoſito, et ſe per caſo il piano terreo non fuße piano, ouer che il perpendicolo caſcaße ſopra alcuna parte di ponto, ouer de diuiſione procederia ſi come nella precedente, et per conoſcer meglio le dette parti ouer frattioni diuidero cadaun ponto, ouer diuiſione, ſi de l’ombra retta come della uerſa (come diſopra fu ancor detto) in altre dodeci parti, et cadauna di quelle chiamaremo minuto: la qual diuiſione mi ſara molto accomoda per trouar le dette altezze, et ancora le diſtantie ypothumiſſale et orizontale ſenza mouermi dal luoco doue me ritrouo.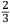 is the number of steps of the length of the mentioned hypotenuse EA, as has been found by means of the previous method, which was to be shown. If it happens that the ground is not flat, that is, that the plumb line falls over a certain point or portion, I then proceed according to the previous proposition. To ascertain the mentioned portions or fractions more precisely, I divide each point or portion of both the right and the horizontal shadow (as has been said above) into a further twelve portions, each of them called a minute. A division of this kind is particularly useful for finding the mentioned heights, hypotenuses and horizontal distances without moving from the place where I am.
is the number of steps of the length of the mentioned hypotenuse EA, as has been found by means of the previous method, which was to be shown. If it happens that the ground is not flat, that is, that the plumb line falls over a certain point or portion, I then proceed according to the previous proposition. To ascertain the mentioned portions or fractions more precisely, I divide each point or portion of both the right and the horizontal shadow (as has been said above) into a further twelve portions, each of them called a minute. A division of this kind is particularly useful for finding the mentioned heights, hypotenuses and horizontal distances without moving from the place where I am.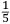 qual ſeruo, poi parto ſimilmente il medemo 12 per 8 (cioè per li ponti che ſega il detto perpendicolo nella ſeconda ſtatione) ne uien 1
qual ſeruo, poi parto ſimilmente il medemo 12 per 8 (cioè per li ponti che ſega il detto perpendicolo nella ſeconda ſtatione) ne uien 1
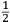 et da questo 1
et da questo 1
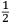 ne ſotro quel 1
ne ſotro quel 1
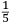 che fu ſeruato reſta
che fu ſeruato reſta
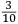 et per questo
et per questo
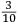 parto 285 (cioè la quantita di piedi che è dal ponto C al punto U) ne uien 950 et a queſto 950 gli agiongo 4 (cioè gli piedi 4 che hauemo ſuppoſto che ſia dal ponto E al ponto C ouer [d]al ponto X
parto 285 (cioè la quantita di piedi che è dal ponto C al punto U) ne uien 950 et a queſto 950 gli agiongo 4 (cioè gli piedi 4 che hauemo ſuppoſto che ſia dal ponto E al ponto C ouer [d]al ponto X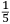 , which I file. I then similarly divide the same 12 by 8 (that is, the point over which the plumb line falls at the second measurement location). It makes 1
, which I file. I then similarly divide the same 12 by 8 (that is, the point over which the plumb line falls at the second measurement location). It makes 1
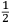 . From this 1
. From this 1
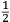 , I subtract 1
, I subtract 1
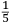 , which was filed, and the difference is
, which was filed, and the difference is
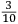 . I divide 285 (that is, the quantity of feet between point C and point U) by this
. I divide 285 (that is, the quantity of feet between point C and point U) by this
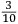 and this makes 950. I then add 4 (that is, the 4 feet we had supposed to be the length from point E to point C, or from point X
and this makes 950. I then add 4 (that is, the 4 feet we had supposed to be the length from point E to point C, or from point X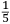 in lo lato LQ. Seguita adonque che il lato AF intra 1
in lo lato LQ. Seguita adonque che il lato AF intra 1
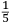 in lo lato EF ſi che ſe ben io non ho alcuna notitia quanto ſia il lato AF ne ancora il lato EF io son certo almen di questo che lo detto lato AF intra come ho detto [1]
in lo lato EF ſi che ſe ben io non ho alcuna notitia quanto ſia il lato AF ne ancora il lato EF io son certo almen di questo che lo detto lato AF intra come ho detto [1]
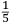 in lo detto lato EF et questo ſeruo da parte, et mi uolto alla ſeconda ſtatione e per le medeme ragioni trouo che lo triangolo XFA è pur ſimile al
in lo detto lato EF et questo ſeruo da parte, et mi uolto alla ſeconda ſtatione e per le medeme ragioni trouo che lo triangolo XFA è pur ſimile al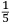 [times] by side LQ. It follows that side AF is contained by side EF 1
[times] by side LQ. It follows that side AF is contained by side EF 1
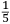 times and, although I do not have any information concerning side AF and side EF, I am still sure about the fact that AF is contained by EF 1
times and, although I do not have any information concerning side AF and side EF, I am still sure about the fact that AF is contained by EF 1
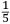
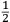 in lo lato LQ (cioè in ponti 12[)] adonque il lato AF intrara ſimilmente 1
in lo lato LQ (cioè in ponti 12[)] adonque il lato AF intrara ſimilmente 1
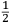 in lo lato XF onde ſotrando il lato EF del lato XF (cioè 1
in lo lato XF onde ſotrando il lato EF del lato XF (cioè 1
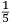 de 1
de 1
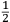 ) reſtara
) reſtara
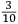 per la differentia EX ſi che la det[ta] differentia EX uerria a eſſer li
per la differentia EX ſi che la det[ta] differentia EX uerria a eſſer li
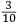 della detta linea AF et perche la detta differentia EX è tanto quanto la linea UC (per la trigeſimaquarta del primo di Euclide) et la detta linea UC é ſuppoſita eſſer piedi 285 ſeguita adonque che queſti piedi 285 ſiano li
della detta linea AF et perche la detta differentia EX è tanto quanto la linea UC (per la trigeſimaquarta del primo di Euclide) et la detta linea UC é ſuppoſita eſſer piedi 285 ſeguita adonque che queſti piedi 285 ſiano li
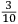 della detta linea AF per il che tutta la linea AF verria a eßer piedi 950 (come che anchora di ſopra fu determinato) giontoui adonque li piedi 4 (che è ſuppoſto eſſer la linea EC ouer XU) farà piedi 954 et piedi 954 dirò che ſia tutta la altezza AB perche FB uien a eſſer ſimilmente piedi 4 che è il primo propoſito. Et perche ſi come lo lato PQ
della detta linea AF per il che tutta la linea AF verria a eßer piedi 950 (come che anchora di ſopra fu determinato) giontoui adonque li piedi 4 (che è ſuppoſto eſſer la linea EC ouer XU) farà piedi 954 et piedi 954 dirò che ſia tutta la altezza AB perche FB uien a eſſer ſimilmente piedi 4 che è il primo propoſito. Et perche ſi come lo lato PQ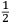 times by side LQ (which is twelve points[)], hence side AF is similarly contained by side XF 1
times by side LQ (which is twelve points[)], hence side AF is similarly contained by side XF 1
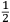 times. Then, by subtracting side EF from side XF (which is 1
times. Then, by subtracting side EF from side XF (which is 1
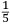 from 1
from 1
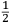 ) it makes
) it makes
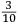 , which is the remaining EX. But the remaining EX is as
, which is the remaining EX. But the remaining EX is as
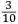 of the mentioned line AF and, since the remaining EX is as long as line UC (based on the thirty-fourth [proposition] of the first [book] of Euclid) and, since the mentioned line UC is supposed to be 285 feet long, it therefore follows that these 285 feet are
of the mentioned line AF and, since the remaining EX is as long as line UC (based on the thirty-fourth [proposition] of the first [book] of Euclid) and, since the mentioned line UC is supposed to be 285 feet long, it therefore follows that these 285 feet are
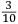 of the entire line AF and, therefore, the entire line AF is 950 feet long (as resulted above). I then add to this result 4 feet (which is the supposed length of line EC or XU), which makes 954 feet. This is the length of the entire height AB, because FB is also 4 feet long, which was to be shown first. Since side PQ
of the entire line AF and, therefore, the entire line AF is 950 feet long (as resulted above). I then add to this result 4 feet (which is the supposed length of line EC or XU), which makes 954 feet. This is the length of the entire height AB, because FB is also 4 feet long, which was to be shown first. Since side PQ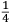 et queſto
et queſto
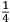 ſeruaria da banda, et dapoi ſegnarò il luoco doue ſon ſtato, cioè farò vn ſegno nel detto piano rettamente ſotto doue cade il piombino del iſtromento. Dapoi me tiraria alquanto in drio, et un’altra volta in queſto ſecondo luoco cercaria la detta ſumita, ouer vertice A per lo traſguardo del detto istromento et dapoi guardaria ſopra a quanti ponti della detta ombra retta caderia el detto mio piombino, et ſe per caſo quel caſcaße ſopra il 4 ponto, io partiria il detto 4 per 12 et me ne veneria
ſeruaria da banda, et dapoi ſegnarò il luoco doue ſon ſtato, cioè farò vn ſegno nel detto piano rettamente ſotto doue cade il piombino del iſtromento. Dapoi me tiraria alquanto in drio, et un’altra volta in queſto ſecondo luoco cercaria la detta ſumita, ouer vertice A per lo traſguardo del detto istromento et dapoi guardaria ſopra a quanti ponti della detta ombra retta caderia el detto mio piombino, et ſe per caſo quel caſcaße ſopra il 4 ponto, io partiria il detto 4 per 12 et me ne veneria
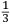 et coſi di queſto
et coſi di queſto
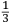 ne cauaria quel
ne cauaria quel
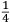 che da prima fu ſaluato, et me ne reſtaria
che da prima fu ſaluato, et me ne reſtaria
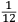 . Dapoi miſuraria diligentemente il ſpacio che ſarà frà la prima et ſeconda ſtatione, cioè da quel ponto ſignato nel piano nel luoco doue riſguardaua il ponto piombino nella prima operatione, a quello doue che riſguardarà nella ſeconda, qual ſpacio pongo per eßempio che fuße paßa 8 io partiria questi paßa 8 per quel
. Dapoi miſuraria diligentemente il ſpacio che ſarà frà la prima et ſeconda ſtatione, cioè da quel ponto ſignato nel piano nel luoco doue riſguardaua il ponto piombino nella prima operatione, a quello doue che riſguardarà nella ſeconda, qual ſpacio pongo per eßempio che fuße paßa 8 io partiria questi paßa 8 per quel
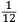 et me ne veneria 96 et à queſto 96 gli aggiongerò quanto ſarà dal pironcino del detto mio istromento per fin in terra, qual pongo che ve ſia I paßo giongeria alli detti paßa 96 quel paßo I et farà 97 paßa et paßa 97 conchiuderia che fuße la detta altezza AB. Et la verità di queſta tal propoſitione ſe dimostra per li medeſimi modi, e uie che fu fatto della prima parte, cioè per la ſimilitudine di triangoli, et delli ſuoi lati proportionali.
et me ne veneria 96 et à queſto 96 gli aggiongerò quanto ſarà dal pironcino del detto mio istromento per fin in terra, qual pongo che ve ſia I paßo giongeria alli detti paßa 96 quel paßo I et farà 97 paßa et paßa 97 conchiuderia che fuße la detta altezza AB. Et la verità di queſta tal propoſitione ſe dimostra per li medeſimi modi, e uie che fu fatto della prima parte, cioè per la ſimilitudine di triangoli, et delli ſuoi lati proportionali.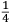 . And I file
. And I file
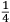 . I then mark the place where I am, that is, I mark the place on the mentioned ground straight under the point where the plumb line of my instrument falls. Then, I move backwards a little bit and target the mentioned top at point A at this second measurement location and through the holes of the mentioned instruments again. Then, I observe over which point on the vertical shadow the plumb line falls. If it happens that it falls on point 4, I divide the mentioned 4 by 12 and this makes
. I then mark the place where I am, that is, I mark the place on the mentioned ground straight under the point where the plumb line of my instrument falls. Then, I move backwards a little bit and target the mentioned top at point A at this second measurement location and through the holes of the mentioned instruments again. Then, I observe over which point on the vertical shadow the plumb line falls. If it happens that it falls on point 4, I divide the mentioned 4 by 12 and this makes
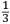 and, thus, from this
and, thus, from this
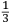 I subtract the
I subtract the
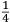 that I had filed before. What remains is
that I had filed before. What remains is
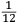 . Then, I diligently measure the space between the first and the second measurement location, that is, from that point marked on the ground under the point where the plumb line fell at the first operation, and the point under the plumb line at the second operation. I suppose this space to be, for example, eight steps long. I divide these 8 steps by that
. Then, I diligently measure the space between the first and the second measurement location, that is, from that point marked on the ground under the point where the plumb line fell at the first operation, and the point under the plumb line at the second operation. I suppose this space to be, for example, eight steps long. I divide these 8 steps by that
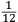 and this makes 96. To this 96, I add that length from the mentioned small pivot down to the ground, which I suppose to be one step. So, I add to the mentioned 96 steps that one step and this makes 97 steps. I conclude that these 97 steps are the height AB. The truth of this proposition is demonstrable by means of the same methods and ways used in the first part, that is, by means of similarity of triangles and proportionality of their sides.
and this makes 96. To this 96, I add that length from the mentioned small pivot down to the ground, which I suppose to be one step. So, I add to the mentioned 96 steps that one step and this makes 97 steps. I conclude that these 97 steps are the height AB. The truth of this proposition is demonstrable by means of the same methods and ways used in the first part, that is, by means of similarity of triangles and proportionality of their sides.